拓扑线性空间
拓扑线性空间(topological)是一类具有拓扑结构的线性空间。如果实数域或复数域 K 上的线性空间E同时是有拓扑 τ 的拓扑空间,并且线性空间的基本运算x+y和αx(x,y∈E,α∈K)分别作为E×E和K×E到E中的映射按 τ 是连续的,则称E为(实或复)拓扑线性空间或拓扑向量空间。而 τ 称为E的线性拓扑或向量拓扑,零元的均衡的领域全体组成零元的邻域基。满足T1分离公理的拓扑线性空间是完全正则的。
拓扑线性空间理论是泛函分析的一个重要分支,其基本概念建立于20世纪30年代,而今已经发展成为一门完整的学科,在纯粹数学和应用数学、理论物理、现代理学和现代工程理论中都有广泛应用。1
局部凸空间局部凸空间(locally convex space)是最重要的一类拓扑线性空间。设E是拓扑线性空间,如果E中存在由均衡凸集组成的零元的邻域基,就称E是局部凸的拓扑线性空间,简称局部凸空间,而E的拓扑称为局部凸拓扑。零元的每个均衡凸邻域V的闵科夫斯基泛函 pv(x) 是E上的连续半范数。反之,设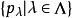 是E上一族半范数,E上使
是E上一族半范数,E上使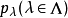 均为连续的最弱拓扑是局部凸的,且零元的均衡凸邻域基由下面形式的集组成
均为连续的最弱拓扑是局部凸的,且零元的均衡凸邻域基由下面形式的集组成
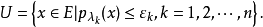 这个局部凸拓扑称为由半范数族
这个局部凸拓扑称为由半范数族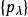 确定的局部凸拓扑。如果对任何
确定的局部凸拓扑。如果对任何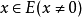 ,都存在
,都存在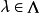 使
使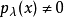 ,则
,则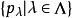 确定的局部凸拓扑是豪斯多夫拓扑。通常局部凸空间都指豪斯多夫局部凸空间。E中的定向半序点列
确定的局部凸拓扑是豪斯多夫拓扑。通常局部凸空间都指豪斯多夫局部凸空间。E中的定向半序点列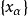 收敛于
收敛于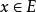 等价于对每个
等价于对每个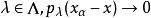 。
。
设E1是由另一半范数族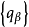 确定的局部凸空间,则使线性映射
确定的局部凸空间,则使线性映射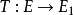 连续的充分必要条件是,对任意的
连续的充分必要条件是,对任意的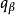 ,总存在有限个
,总存在有限个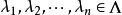 和常数c,使不等式
和常数c,使不等式
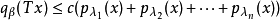 对一切
对一切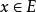 成立。
成立。
局部凸空间的完备化空间也是局部凸的。根据哈恩-巴拿赫泛函延拓定理,局部凸空间上存在足够多的非零连续性泛函。正因为如此,局部凸空间理论成为拓扑线性空间理论中最重要的部分。
关于局部凸空间理论的发展大约是始于迪厄多内(Dieudonné,J.)和施瓦兹(Schwarz,L.)在1949年的工作,它的一个主要推动力是分布理论,即广义函数理论。1
自反局部凸空间自反局部凸空间(reflexive locally convex space)属于一类局部凸空间。设E是局部凸空间,则赋予强拓扑的共扼空间E'的共扼空间E''包含原来的空间E,当E" = E时,称E是半自反的。进一步当E的拓扑和强拓扑β(E,E')一致时,称E为自反的。E为半自反的充分必要条件是E的任意有界弱闭凸集是弱紧的。E为自反的充分必要条件是E为半自反的且是拟桶型的。对于赋可列范线性空间,自反和半自反是一致的。1
拟桶型空间拟桶型空间(quasi-barreled space)是桶型空间概念的推广。设E是局部凸空间,E中的子集A称为拟桶集,是指A是吸收一切有界集的桶集。如果E中每个拟桶集都是零元的邻域,则称E为拟桶型空间。局部凸空间为拟桶型空间的充分必要条件是在每个有界集上的下半连续半范数是连续的。1




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国