[科普中国]-盖尔范德积分

盖尔范德积分亦称盖尔范德意义下的弱*积分，是一种向量值函数的积分，此积分是由盖尔范德于1936年建立的。

简介盖尔范德积分亦称盖尔范德意义下的弱*积分，是一种向量值函数的积分，此积分是由盖尔范德于1936年建立的。1

设(Ω,𝓕,μ)是σ有限测度空间，x(t)是定义在Ω上而取值于巴拿赫空间X的向量值函数。如果对每个f∈X*，f(x(t))在Ω上是μ可积的，则必存在x**∈X，使得对于每个f∈X*有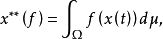x**称为x(t)在Ω上的盖尔范德积分，记为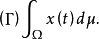

提出者盖尔范德，苏联数学家，生物学家，1913年9月2日生于乌克兰敖德萨省。 1932年，年仅19岁的盖尔范德被录取为莫斯科大学的研究生，师从柯尔莫哥洛夫。 1940年，盖尔范德获苏联物理数学科学博士学位，在学位论文中，他创建了赋范环论，即巴拿赫代数论。 1943年，盖尔范德开创了 C *代数的研究并开始担任莫斯科大学教授。 1958年以后，盖尔范德几乎不再独自进行研究，但与很多人有着合作的关系。

事实上，在盖尔范德一生发表的论文中，只有33篇以他个人的名义发表，而同他联名发表论文的作者，共有206位(包括中国数学家夏道行)，合作发表50篇以上者2位；20至49篇者5位；10至19篇者22位；5至9篇者21位。 论文涉及的领域也十分广泛，包括巴拿赫代数、调和分析、群表示论、积分几何、广义函数、无穷维李代数的上同调、微分方程、生物学和生理学。

向量值函数一元函数是一个由定义域到值域的映射，其定义域与值域都是一维数集。

向量值函数是指分量都是关于同一自变量的一元函数，就是说 n 元向量值函数是x到xn上的映射。我们感兴趣的是取值为二维和三维的向量值函数，即n=2和n=3的情形。

本词条内容贡献者为:

宋春伟 - 教授 - 北京大学