抽象积分(abstract integral)是勒贝格积分的进一步抽象,是现代分析数学中的重要工具之一。设(Ω,F,μ)是测度空间,f(x)是(Ω,F)中的可测函数,建立抽象积分∫Ωf(x)dμ的步骤与建立勒贝格积分或勒贝格-斯蒂尔杰斯积分的步骤基本相同,只需在定义中将勒贝格测度换成一般测度μ,相应的非负简单函数、非负可测函数、一般可测函数换成测度空间中的同名函数即可。对于积分存在和可积两个概念也做类似定义,当(Ω,F,μ)是完备测度空间时,抽象积分的性质与勒贝格积分的性质基本相同,也有关于积分收敛性的三大定理(列维定理、法图引理、勒贝格控制收敛定理)。也可以引进平均收敛等概念,并且与几乎处处收敛、依测度收敛、近于一致收敛的关系也一样,仅需做明显的文字和记号修改。
基本介绍积分的概念可从不同的观点出发向各种不同的方向抽象化。它大致可以分为两个方向,一个方向是对取值于局部凸拓扑线性空间(不一定是数空间)的函数或测度定义积分(简称为在拓扑线性空间上的积分),另外一个方向是把和序关系有关的积分抽象化。下面对各方向取其有代表性的两个积分予以叙述。
拓扑线性空间上的积分**拓扑线性空间上的积分(Bochner积分)**设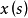 为定义在
为定义在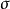 有限测度空间
有限测度空间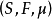 上,取值于Banach空间X中的函数,如果在使
上,取值于Banach空间X中的函数,如果在使
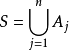 的互不相交的F可测集
的互不相交的F可测集 上,
上,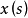 x(s)分别取常量
x(s)分别取常量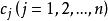 ,就称它为阶梯函数(step function)或有限值函数(finite-valued function)。使用
,就称它为阶梯函数(step function)或有限值函数(finite-valued function)。使用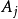 的定义函数
的定义函数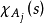 ,可以把这个阶梯函数表示为
,可以把这个阶梯函数表示为
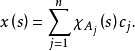 如果对于
如果对于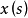 能选取适当的阶梯函数序列
能选取适当的阶梯函数序列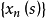 ,使得在S上对几乎一切s,
,使得在S上对几乎一切s,
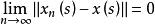 成立,则称
成立,则称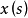 为强可测的(strongly measurable)。当
为强可测的(strongly measurable)。当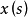 为强可测,且
为强可测,且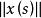 作为S上的实值函数为Lebesgue可积时,则定义
作为S上的实值函数为Lebesgue可积时,则定义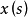 为Bochner可积的(Bochner integrable)(由
为Bochner可积的(Bochner integrable)(由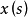 的强可测性可以得到
的强可测性可以得到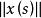 的可测性)。特别当
的可测性)。特别当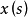 是Bochner可积的阶梯函数
是Bochner可积的阶梯函数
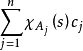 时,其Bochner积分定义为
时,其Bochner积分定义为
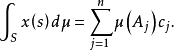 一般地说,对于Bochner可积函数
一般地说,对于Bochner可积函数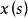 ,可以证明,存在满足下列条件的Bochner可积的阶梯函数序列
,可以证明,存在满足下列条件的Bochner可积的阶梯函数序列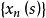 :
:
i)对几乎一切S,
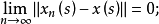
ii)
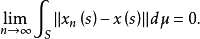 (例如,由
(例如,由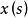 的强可测性得到,存在阶梯函数序列
的强可测性得到,存在阶梯函数序列 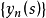 ,对几乎一切s,它强收敛于
,对几乎一切s,它强收敛于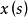 ,对此
,对此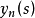 ,如下地定义阶梯函数序列
,如下地定义阶梯函数序列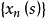 :当
:当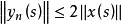 时,令
时,令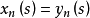 ;当
;当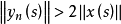 时,令
时,令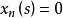 ;则
;则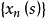 满足上述条件i),ii)。)从而对于这样的
满足上述条件i),ii)。)从而对于这样的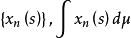 强收敛,且其极限不依赖于
强收敛,且其极限不依赖于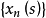 的选择方法。而
的选择方法。而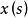 的Bochner积分(Bochner integral),就定义为
的Bochner积分(Bochner integral),就定义为
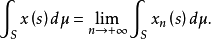 为了和其他积分加以区别,有时把Bochner积分写作
为了和其他积分加以区别,有时把Bochner积分写作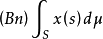 。Bochner可积函数在任意的F可测集上都是Bochner可积的,除此之外,Lebesgue积分的几乎所有性质(线性,完全可加性,绝对连续性,Lebesgue收敛定理,Fubini定理等),把绝对值换以范数之后都照样成立。但是Radon-Nikodym定理不成立。当T是由Banach空间X到Banach空间Y的连续线性算子时,若S上取值于X中的函数
。Bochner可积函数在任意的F可测集上都是Bochner可积的,除此之外,Lebesgue积分的几乎所有性质(线性,完全可加性,绝对连续性,Lebesgue收敛定理,Fubini定理等),把绝对值换以范数之后都照样成立。但是Radon-Nikodym定理不成立。当T是由Banach空间X到Banach空间Y的连续线性算子时,若S上取值于X中的函数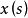 是Bochner可积的,则
是Bochner可积的,则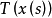 作为S上取值于Y中的函数是Bochner可积的,且
作为S上取值于Y中的函数是Bochner可积的,且
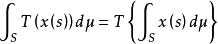 成立。特别当S是n维Euclid空间时,Bochner积分具有强可微性1。
成立。特别当S是n维Euclid空间时,Bochner积分具有强可微性1。
Birkhoff积分Birkhoff积分是关于在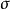 有限测度空间
有限测度空间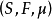 上定义的,在Banach空间X中取值的函数
上定义的,在Banach空间X中取值的函数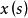 ,按Lebesgue积分的构造方法定义的积分。首先,对于X的元的可列族
,按Lebesgue积分的构造方法定义的积分。首先,对于X的元的可列族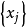 ,当级数
,当级数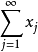 在其各项的次序任意改变之后仍然强收敛时,称
在其各项的次序任意改变之后仍然强收敛时,称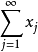 为无条件收敛(unconditionally converge)。当
为无条件收敛(unconditionally converge)。当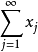 无条件收敛时,可以证明,它的和不依赖于相加的顺序,总是一定的。特别当X是数空间时,无条件收敛和绝对收敛的概念是一致的;但一般地说,无条件收敛的级数并不一定绝对收敛(绝对收敛是指
无条件收敛时,可以证明,它的和不依赖于相加的顺序,总是一定的。特别当X是数空间时,无条件收敛和绝对收敛的概念是一致的;但一般地说,无条件收敛的级数并不一定绝对收敛(绝对收敛是指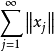 收敛)。给定S的一个可列分割
收敛)。给定S的一个可列分割
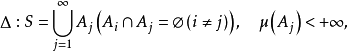 若函数
若函数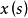 在每个
在每个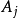 上有界且
上有界且
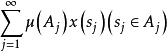 无条件收敛,则称
无条件收敛,则称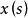 关于
关于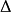 可求和,此种和的全体
可求和,此种和的全体
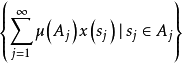 的凸闭包,称为
的凸闭包,称为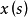 对于△的积分值域(integral range),记作
对于△的积分值域(integral range),记作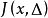 。于是,如果对任意的正数
。于是,如果对任意的正数 ,可选取S的可列分割△,使
,可选取S的可列分割△,使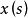 关于△可求和,且
关于△可求和,且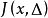 的直径小于
的直径小于 ,则称
,则称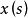 为Birkhoff可积的(Birkhoff integrable)。若
为Birkhoff可积的(Birkhoff integrable)。若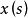 关于某一可列分割△可求和,则可以证明,它对△的任一加细
关于某一可列分割△可求和,则可以证明,它对△的任一加细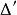 仍然是可求和的,且
仍然是可求和的,且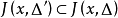 。从而当
。从而当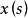 是Birkhoff可积时,
是Birkhoff可积时,
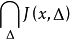 成为只含有X的一个点的集合。此
成为只含有X的一个点的集合。此
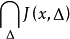 定义为
定义为 的Birkhoff积分(Birkhoff integral),写作
的Birkhoff积分(Birkhoff integral),写作
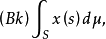 或简写为
或简写为
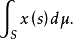 Birkhoff可积函数在任意的F可测子集上仍为Birkhoff可积函数。Birkhoff积分作为集函数具有完全可加性和绝对连续性,对于被积函数具有线性性质。但Fubini定理不成立。又对于收敛定理来说不能得到Bochner积分那样好的结果,Bochner可积函数必是Birkhoff可积的,但其逆不成立。
Birkhoff可积函数在任意的F可测子集上仍为Birkhoff可积函数。Birkhoff积分作为集函数具有完全可加性和绝对连续性,对于被积函数具有线性性质。但Fubini定理不成立。又对于收敛定理来说不能得到Bochner积分那样好的结果,Bochner可积函数必是Birkhoff可积的,但其逆不成立。
以此Birkhoff积分的构造法为基础,G.Birkhoff和R.S.Phillips对取值于局部凸拓扑线性空间中的函数的积分作了定义。用此种积分的理论,使得Birkhoff积分成为这种积分基于在Banach空间上引人拓扑的方法,不同而得到的特殊情形。 进一步C.E.Rickart把Birkhoff积分推广到取值为局部凸拓扑线性空间的子集的函数,并求得了Radon-Nikodym定理1。
本词条内容贡献者为:
尚华娟 - 副教授 - 上海财经大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国