[科普中国]-复值可测函数

设(Ω,𝓕)为可测空间，若f1(x)，f2(x)都是(Ω,𝓕)上的实值可测函数，则称f(x)=f1(x)+if2(x)为其上的复值可测函数。

简介复值可测函数是复值勒贝格可测函数概念的推广。

设(Ω,𝓕)为可测空间，若f1(x)，f2(x)都是(Ω,𝓕)上的实值可测函数，则称f(x)=f1(x)+if2(x)为其上的复值可测函数。1

可测空间(measurable space)

可测空间是测度论中的基本概念，可测空间和定义在可测空间上的测度构成测度空间。可测空间是测度的定义域，在一个可测空间上可以定义不止一种测度。

设X是一个非空集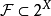，是X的一个σ代数，称（X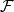，）为一个可测空间。每个集合A∈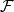是（X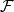，）中的可测集，也称为X中的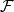可测集，简称可测集。

勒贝格可测函数勒贝格可测函数简称(L)可测函数，是比连续函数更广的一类函数。

定义在(L)零测度集上的任何实值函数以及区间上的半连续函数都是(L)可测函数。定义在(L)可测集上的任何连续函数都是(L)可测函数。

本词条内容贡献者为:

李嘉骞 - 博士 - 同济大学