分类
上同调运算包括平展上同调(Étale cohomology),德拉姆上同调(de Rham cohomology),李代数上同调,伽罗瓦上同调,霍赫希尔德同调。1
平展上同调在数学中,一个代数簇或概形的平展上同调(Étale cohomology)是一个与一般拓扑空间的有限系数上同调群类似的代数结构。这一概念作为证明韦伊猜想的工具由亚历山大·格罗滕迪克引入。平展上同调的理论可以用于构建ℓ进上同调,后者则是代数几何中韦伊上同调理论的一个例子。这一理论有着众多的应用,包括Weil猜想的证明以及李型有限单群的表示的构造。
目的对于复代数簇,代数拓扑中的某些不变量(例如基本群和上同调)是非常有用的,因此自然地我们希望为其他域(例如有限域)上的代数簇也定义类似的概念。(特别地,韦伊指出了这样的上同调理论可以用于证明韦伊猜想。)对于凝聚层的上同调,塞尔指出仅利用代数簇上的扎里斯基拓扑就可以进行定义,而且在复代数簇的情况下,这样的定义可以与(更细致的)复数拓扑导出相同的上同调群。但是,对于常值层(例如整数层),这样的定义则不适用,因为使用扎里斯基拓扑定义的上同调群效果不佳。例如,韦伊希望可以为有限域上的簇构造一个上同调理论,使其拥有与拓扑空间的奇异上同调有类似的效力;但实际上,任何不可约簇上的常值层都有着平凡的上同调群(所有高阶上同调群都是平凡的)。
扎里斯基拓扑之所以不适用,是因为它过于粗糙:它包含的开集过少。另一方面,为任意的代数簇赋予更细致的拓扑似乎也并不可行。格罗滕迪克的创见则在于认识到广义的开集并不需要是代数簇的子集:层的定义并不需要限制于开子集范畴,事实上它对于任何范畴都一样适用。于是,格罗滕迪克将开子集范畴替换为平展态射范畴,并由此定义了平展上同调。粗略地来说,平展态射可以被看作空间的有限非分支覆盖上的开集。这样的构造,(经过大量的工作之后),被证明提供了恰好足够多的开集,使得常系数上同调群(特别地,对于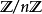 ,其中n与域特征互质)有良好的性质。
,其中n与域特征互质)有良好的性质。
一些基本的直观理解如下:
若隐函数定理在代数几何中为真,则平展条件可被看作该定理的前提。(注意隐函数定理在一般的代数几何中并不为真)
对于阿贝尔簇,在0和1维的情况下,一些常系数层的基本情况可以用其他理论(例如伽罗瓦上同调和泰特模)来预测。
定义令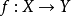 为一个概形之间的态射,
为一个概形之间的态射,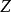 为一个Y-概形,J为一个Z上的幂零理想层(nilpotent sheaf of ideals),
为一个Y-概形,J为一个Z上的幂零理想层(nilpotent sheaf of ideals), 为
为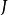 所确定的闭浸入。我们称
所确定的闭浸入。我们称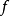 是形式平展的,若对于所有的Y-态射
是形式平展的,若对于所有的Y-态射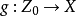 ,都存在唯一的Y-态射
,都存在唯一的Y-态射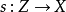 使得
使得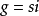 。我们称
。我们称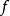 是局部有限表示的,若对于
是局部有限表示的,若对于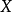 的每一点
的每一点 , 都有一个
, 都有一个 的邻域
的邻域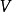 和
和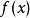 的邻域
的邻域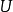 使得
使得 而且
而且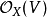 是一个
是一个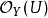 上的有限表示代数(即,前者可被看作后者的一个有限多项式环约去一个有限生成理想所得到的商代数)。一个形式平展且局部有限表示的态射被成为一个平展态射(Étale morphism)。等效地,一个平坦(flat)且非分歧(unramified)的态射是一个平展态射(参见:概形论术语)。
上的有限表示代数(即,前者可被看作后者的一个有限多项式环约去一个有限生成理想所得到的商代数)。一个形式平展且局部有限表示的态射被成为一个平展态射(Étale morphism)。等效地,一个平坦(flat)且非分歧(unramified)的态射是一个平展态射(参见:概形论术语)。
对于任何一个概形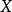 ,令
,令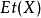 表示其全部平展态射组成的范畴。注意到它与概形的关系类似于开子集范畴与拓扑空间的关系,而该范畴的对象则可以被(非正式地)看成是X的“平展开子集”。拓扑空间中两个开集的交集则可以看成两个平展态射的拉回。稍微需要注意的一点细节是
表示其全部平展态射组成的范畴。注意到它与概形的关系类似于开子集范畴与拓扑空间的关系,而该范畴的对象则可以被(非正式地)看成是X的“平展开子集”。拓扑空间中两个开集的交集则可以看成两个平展态射的拉回。稍微需要注意的一点细节是 并非是一个小范畴;但是因为平展态射是局部有限表示的,将其视作小范畴亦无妨。
并非是一个小范畴;但是因为平展态射是局部有限表示的,将其视作小范畴亦无妨。
 一个拓扑空间上的预层是一个从开子集范畴到集合范畴(
一个拓扑空间上的预层是一个从开子集范畴到集合范畴(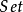 )的逆变函子;类似地,我们定义一个概形的平展预层为从
)的逆变函子;类似地,我们定义一个概形的平展预层为从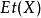 到
到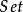 的一个逆变函子。一个预层被称为层,若层条件(当一个开集
的一个逆变函子。一个预层被称为层,若层条件(当一个开集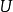 被
被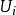 覆盖,且
覆盖,且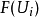 均被给定,使得所有的这些
均被给定,使得所有的这些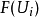 在任意的
在任意的 上都有一致的取值,则
上都有一致的取值,则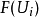 都是唯一的某个
都是唯一的某个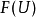 的像)可以得到满足;因此类似地,我们称一个平展预层为平展层,若对应的平展层条件得到满足。(这里“并集”被平展映射的拉回代替,而“
的像)可以得到满足;因此类似地,我们称一个平展预层为平展层,若对应的平展层条件得到满足。(这里“并集”被平展映射的拉回代替,而“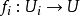 覆盖
覆盖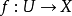 ”则被定义为
”则被定义为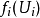 覆盖
覆盖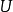 。)对于任何范畴上的格罗滕迪克拓扑,我们都可以类似地定义层的概念。
。)对于任何范畴上的格罗滕迪克拓扑,我们都可以类似地定义层的概念。
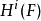 因为一个概形上的阿贝尔层(取值为阿贝尔群的层)的范畴包含足够多的单射对象,我们可以在其上定义左正合函子的右导出函子。对于一个阿贝尔层的范畴
因为一个概形上的阿贝尔层(取值为阿贝尔群的层)的范畴包含足够多的单射对象,我们可以在其上定义左正合函子的右导出函子。对于一个阿贝尔层的范畴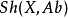 ,其全局截面函子是一个映射
,其全局截面函子是一个映射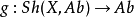 ,将每个层
,将每个层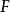 映射到其全局截面(也就是
映射到其全局截面(也就是 )。给定一个阿贝尔层
)。给定一个阿贝尔层 ,定义其平展上同调群为
,定义其平展上同调群为 的右导出函子
的右导出函子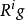 在
在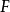 上的值。特别地,
上的值。特别地, 便是
便是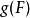 。
。
更为一般地,若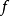 是一个从
是一个从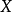 到
到 的概形态射,则有
的概形态射,则有 函子从X的平展层映射到Y的平展层,而其右导出函子则被写为
函子从X的平展层映射到Y的平展层,而其右导出函子则被写为 。若Y是一个代数闭域的谱(也就是一个点),则
。若Y是一个代数闭域的谱(也就是一个点),则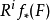 与
与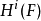 相同。
相同。
令X为诺特概形。若一个X的阿贝尔平展层被X的一个平展覆盖所表示,则我们称其为有限局部常值的。若X可被有限个子概形覆盖,且F在每个子概形上都是有限局部常值的,则称F为可构造的。若对于任何X的平展覆盖U,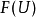 都是挠群,则称F为挠的。自然地,有限局部常值的层都是可构造的,而可构造层都是挠的。每一个挠层都是一个可构造层的滤子归纳极限。
都是挠群,则称F为挠的。自然地,有限局部常值的层都是可构造的,而可构造层都是挠的。每一个挠层都是一个可构造层的滤子归纳极限。
性质大致上,ℓ进上同调群与复数簇的奇异上同调群有类似的性质,区别在于前者是ℓ进数(或ℓ进有理数)的模而后者是整数(或有理数)的模。在非奇异射影簇上,庞加莱对偶性成立,且复数簇的“模p约化”的ℓ进上同调群与奇异上同调群多数情况下有同样的秩。Künneth公式同样也成立。
例如,一个复椭圆曲线的第一上同调群是一个秩为2的整数自由模,而一个有限域椭圆曲线的第一ℓ进上同调群则是一个秩为2的ℓ进数自由模(只要ℓ不是该有限域的特征),而且后者与泰特模对偶。
ℓ进上同调群在一个意义上优于奇异上同调群:前者往往受伽罗瓦群作用。例如,若一个复数簇在有理数上定义,则其ℓ进上同调群受有理数的绝对伽罗瓦群的作用,因此是一个伽罗瓦表示。
有理数的伽罗瓦群的元素(除去平凡元和共轭元之外),大多不在有理数上定义的复数簇上有连续作用,因此大多不在奇异上同调群上作用。这一现象与拓扑空间的基本群在奇异上同调群上作用的事实有关,因为格罗滕迪克证明了伽罗瓦群可以被视作某种形式的基本群。2
霍赫希尔德同调概述数学中,霍赫希尔德同调(Hochschild homology)是环上结合代数的同调论。对某些函子也有一个霍赫希尔德同调。这是以德国数学家格哈德·霍赫希尔德(Gerhard Hochschild)冠名的。
代数的霍赫希尔德同调之定义设k是一个环,A是一个结合k-代数,M是一个A-双模。我们记A为A在k上的n重张量积。给出霍赫希尔德同调的链复形是
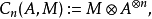 边缘算子di定义为
边缘算子di定义为
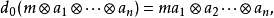
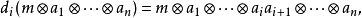
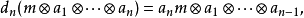 这里对所有 1 ≤i≤n,ai属于A,而m∈M。如果我们令
这里对所有 1 ≤i≤n,ai属于A,而m∈M。如果我们令
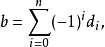 则b°b= 0,所以 (Cn(A,M),b) 是一个链复形,叫做霍赫希尔德复形,它的同调是A系数取M的霍赫希尔德同调。
则b°b= 0,所以 (Cn(A,M),b) 是一个链复形,叫做霍赫希尔德复形,它的同调是A系数取M的霍赫希尔德同调。
伽罗瓦上同调 在数学中,伽罗瓦上同调是一套用群上同调研究伽罗瓦群的作用的技术。具体言之,假设伽罗瓦群
在数学中,伽罗瓦上同调是一套用群上同调研究伽罗瓦群的作用的技术。具体言之,假设伽罗瓦群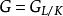 作用在一个群
作用在一个群 (通常是数论中出现的代数结构,如
(通常是数论中出现的代数结构,如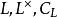 等等)上,伽罗瓦上同调研究相关的群上同调。这些群通常具有重要的数论或算术代数几何意义。
等等)上,伽罗瓦上同调研究相关的群上同调。这些群通常具有重要的数论或算术代数几何意义。
伽罗瓦上同调是现代代数数论的基石之一。
在代数数论中的应用伽罗瓦上同调最早在1950年代被提出,主要与克劳德·谢瓦莱在类域论上的工作相关。这套理论的目的在以群上同调“代数地”阐释类域论,避免使用L-函数。哈瑟原理在伽罗瓦上同调的框架下能得到清晰的描述。
在代数几何中的应用伽罗瓦上同调关系到算术代数几何中的许多重要问题,例如椭圆曲线上的整点个数。作为下降理论在平展拓扑上的应用,第一个伽罗瓦上同调群分类了概形{\displaystyle \mathrm {Spec} (K)}上的扭子,这是主丛在代数几何上的推广。借着下降理论,可以用伽罗瓦上同调研究二次型式、中心单代数与 Severi-Brauer 簇等等结构。3
李代数上同调在数学中,李代数上同调是李代数的一种上同调理论,由谢瓦莱和艾伦伯格为了对紧李群的拓扑空间的上同调进行代数构造而建立。在上文提及的论文中,一个特定的被称作Koszul复形的特殊复形,在李代数的模上定义,而其上同调则以一般形式被构造。
动机令G为一个紧李群,则其被对应的李代数完全确定,因此由李代数来确定李群上同调应为可能的。我们使用如下的构造。注意到李群的上同调是G上的微分形式构成的复形对应的德拉姆上同调,而这个复形可以被替换为等变微分形式的复形,而后者则可以被看作带有一个合适的微分算子的李代数的外代数。这一微分算子的构造对于任何李代数都成立,因此被用于定义所有李代数的李代数上同调。更加一般化地,我们可以用类似的构造来定义模系数的李代数上同调。
定义令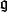 是一个交换环R上的一个李代数,其泛包络代数为
是一个交换环R上的一个李代数,其泛包络代数为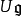 ;令M为
;令M为 的一个表示(或者,等效地,
的一个表示(或者,等效地, 的一个模)。将R考虑为
的一个模)。将R考虑为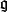 的一个平凡表示,则可以构造上同调群
的一个平凡表示,则可以构造上同调群
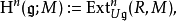 (参见Ext函子)。等效地,我们可以将其看作下面这个左正合不变子模函子的右导出函子:
(参见Ext函子)。等效地,我们可以将其看作下面这个左正合不变子模函子的右导出函子:
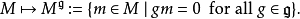 类似地,可以定义李代数同调群为
类似地,可以定义李代数同调群为
 (参见Tor函子)。我们也可以将其看作下面这个右正合协不变函子的左导出函子:
(参见Tor函子)。我们也可以将其看作下面这个右正合协不变函子的左导出函子:
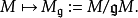
李代数上同调的重要基本结果包括:怀特海德引理,外尔定理和莱维分解定理。4
德拉姆上同调概述数学上,德拉姆上同调(de Rham cohomology)是同时属于代数拓扑和微分拓扑的工具。它能够以一种特别适合计算和用具体的上同调类的方式表达关于光滑流形的基本拓扑信息。它是基于有特定属性的微分形式的存在性的上同调理论。它以不同的确定的意义对偶于奇异同调,以及亚历山大-斯潘尼尔上同调。
定义任何光滑流形M上的光滑微分k-形式在加法之下形成一个交换群(实际上也是一个实向量空间,称为Ω(M)。外导数d给了以下的映射d:Ω(M) → Ω(M).下面是一个基本的关系d=0;这本质上是因为二阶导数的对称性。所以k-形式和外导数形成一个上链复形(cochain complex),称为de Rham复形:
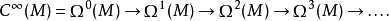
微分几何术语中,是其它微分形式的外导数的形式称为恰当形式(exact form),而外导数为0的形式称为闭形式(参看闭形式和恰当形式);d=0这个关系说明恰当的微分形式都是闭的。5




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国