[科普中国]-概率测度

简介

概率测度(probability measure)是概率论、遍历理论等数学分支中常用的一种重要的有限测度。

在数学中，概率测度是在满足测度属性（如可加性）的概率空间中的一组事件上定义的实值函数。概率测度与一般的测度概念（包括像面积或体积等概念）之间的差异在于：概率测量整个概率必须为1。

直观地，加和性表明，通过测度分配给两个不相交事件的并集的概率应该是事件的概率的总和。例如， 在一个模具的投掷中分配给“1或2”的概率值应该是分配给“1”和“2”的概率值的总和。

概率测度在物理学，财务和生物学领域都有应用。1

定义函数μ作为概率空间，它的概率测度的要求是：

（1）μ必须以在[0，1]之内返回结果，返回0为空集，返回1为整个空间。

（2）μ必须满足所有可数集合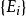中不相交集合可加的属性：

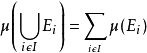
例如，给定概率为1/4，1/4和1/2的三个元素1,2和3，分配给{1,3}的值为1/4 + 1/3 = 3/4，如下图。

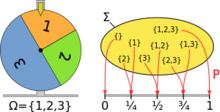
基于事件交点的条件概率定义为：

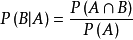
只要P（A）不为零，就满足概率测度要求。

概率测度与模糊测度的概念不同，其中模糊值不需要总和为1，并且添加属性由基于集合包含的顺序关系替代。2

示例应用基于实际市场变化将金融市场进行概率分配是数学融资中所关注的概率测度的一个例子。 在金融衍生品的定价中，例如，风险中性措施是一种概率测度，它假设资产的当前价值是相对于同样的风险中性量度（即使用相应的风险中性密度函数计算）的未来收益的预期值，以无风险利率体现。 如果有一个概率测度，必须用于对市场中的资产进行定价，那么市场就被称为一个完整的市场。

不是所有直观地可能都是概率测度。 例如，虽然统计力学系统的基本概念是度量空间，但这些并不总是概率测度。一般来说，在统计物理学中，如果我们考虑“系统S假设状态A为p的概率”的句子，那么系统的几何并不总是导致在一致性下的概率测量的定义。

概率测量也用于数学生物学，例如，在比较序列分析中，概率测量可以针对序列中的氨基酸允许的变体可能性来定义。

延伸勒贝格测度在测量理论中，勒贝格测度（Lebesgue measure）是将测度分配给n维欧几里德空间子集的标准方法。 对于n = 1，2或3时，它可以对长度，面积或体积进行标准度量。 一般来说，它也称为n维体积，n-体积或简单体积。它可以在实际分析中使用，特别是在定义勒贝格积分时得到应用。勒贝格测度通常表示为dx。

给定一个欧几里德空间中的子集E，定义区间I=[a，b]且区间长度为L(I)=b-a，满足E包含于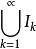，则E的勒贝格外部测度为：

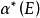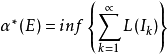
勒贝格测度是在勒贝格σ代数上定义的，它是所有满足条件的子集E的集合，条件为，对于每个欧几里德空间的子集A有：

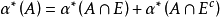
对于勒贝格σ代数中的任何集合，其勒贝格测度均由其勒贝格外部测度给定：

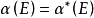
不包含在勒贝格σ代数的集合不是勒贝格可测度的。

一般地，实数的任何闭区间[a，b]是勒贝格可测度的，其勒贝格测度是长度b - a。开区间（a，b）的勒贝格测度同上，这是因为两组之间的差异仅由端点a和b组成。3

区间[a，b]和[c，d]的任意笛卡尔乘积是勒贝格可测度的，其勒贝格测度是（b-a）（d-c），代表相应矩形的面积。

任何可数的实数集的勒贝格测度均为0。

如果确定性公理成立，那么所有的集体都是勒贝格可测度的。

简单平面曲线的图像也是勒贝格可测度的。

博雷尔测度在数学中，特别是在测量理论中，拓扑空间上的博雷尔测度（Borel measure）是在所有开放集合（以及所有Borel集合）上定义的度量。

定义X为豪斯多夫空间的集合，B(X)为包含X中所有开集合的最小σ代数，这被称为博雷尔集合的σ代数。博雷尔测度是在伯雷尔集合的σ代数上定义的任何测度。

一般地，欧几里得空间R与其通常的拓扑结构是一个局部紧凑的Hausdorff空间，因此我们可以定义一个博雷尔测度。在这种情况下，B(R)为包含R中所有开集合的最小σ代数，这被称为博雷尔集合的σ代数。虽然理论上会存在很多Borel测度μ，但是对于半开区间(a，b]的博雷尔测度恒为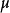=((a，b])=b-a。这一测度结果表明，被定义在博雷尔σ代数上的博雷尔测度，同样被定义在勒贝格σ代数上。由此可见，博雷尔测度和勒贝格测度在博雷尔集合上的测度结果一致，对于每一个博雷尔可测度的集合，均满足。

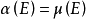使概率测度与勒贝格测度相关联的变量是概率密度函数，具体原理为拉东-尼古丁定理。

博雷尔测度与对定义在其上的集合的勒贝格测度结果一致， 然而还有比博雷尔可测集更多的勒贝格可测量集。博雷尔测度不变量，但不完整。