勒让德条件(Legendre condition)是勒让德(A.-M.Legendre)于1786年得到的。对于一个给定的最简泛函,要检验维尔斯特拉斯条件是否成立,一般是比较困难的,勒让德条件是一种能代替维尔斯特拉斯条件的比较容易检验的条件。勒让德条件也是泛函取得极值的必要条件。
定义勒让德条件是弱极值的一个必要条件,平稳函数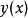 使泛函
使泛函
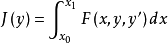 取极小值(或极大值)的必要条件是
取极小值(或极大值)的必要条件是
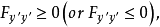 称其为勒让德条件。此外,若沿着场的平稳曲线满足条件
称其为勒让德条件。此外,若沿着场的平稳曲线满足条件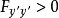 ,则称为严格勒让德条件。若
,则称为严格勒让德条件。若
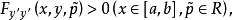 则称为强勒让德条件。
则称为强勒让德条件。
对一般的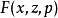 ,勒让德条件是
,勒让德条件是
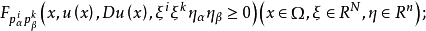 对强勒让德条件,“≥”改为“>”1。
对强勒让德条件,“≥”改为“>”1。
相关介绍对于一个给定的最简泛函,要检验魏尔斯特拉斯条件是否成立,一般情况下比较困难。所以希望能用一个比较简单的条件来代替魏尔斯特拉斯条件。
设最简泛函
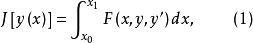 其边界条件为
其边界条件为
 式中,被积函数
式中,被积函数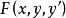 具有连续二阶偏导数。将被积函数
具有连续二阶偏导数。将被积函数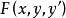 关于变元
关于变元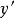 在
在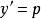 处展成泰勒公式
处展成泰勒公式
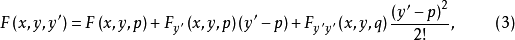 式中,q介于p和
式中,q介于p和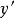 之间。
之间。
将式(3)代入魏尔斯特拉斯函数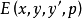 中,得
中,得
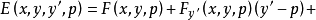
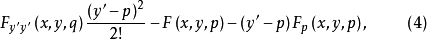 因
因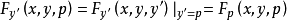 ,故式(4)成为
,故式(4)成为
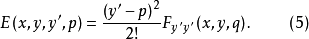
可见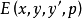 与
与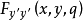 具有相同的符号,故魏尔斯特拉斯条件可用下面的条件来代替
具有相同的符号,故魏尔斯特拉斯条件可用下面的条件来代替
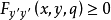 (或
(或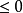 ).
). 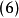
式(6)是勒让德于1786年通过研究二次变分提出来的,称为泛函式(1)的勒让德条件。如果式(6)是严格的不等式,则称为勒让德强条件。勒让德条件也是泛函取得极值的必要条件。泛函的一条极值曲线包含在极值曲线场中的充分条件是必须满足勒让德强条件。
相关定理设泛函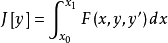 ,其边界条件为
,其边界条件为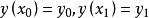 ,其中
,其中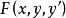 具有连续二阶偏导数,并设
具有连续二阶偏导数,并设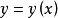 为该泛函的极值函数,若满足下列条件:
为该泛函的极值函数,若满足下列条件:
(1)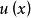 为雅可比方程的解,且
为雅可比方程的解,且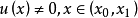 ;
;
(2) 在区间
在区间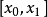 内有
内有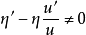 ;
;
(3)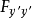 在区间
在区间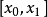 内不变号;
内不变号;
那么当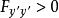 时,
时,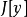 为弱极小值;当
为弱极小值;当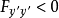 时,
时,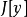 为弱极大值。
为弱极大值。
例题解析例1 试判断泛函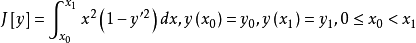 的勒让德条件是否成立。
的勒让德条件是否成立。
解: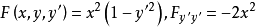 。当
。当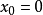 时,勒让德条件成立。当
时,勒让德条件成立。当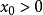 时,勒让德强条件成立。
时,勒让德强条件成立。
例2 设泛函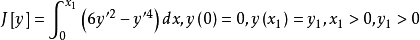 。试判断该泛函的极值曲线是否能包含在一个相应的极值曲线场中。
。试判断该泛函的极值曲线是否能包含在一个相应的极值曲线场中。
**解:**因泛函只是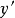 的函数,故其欧拉方程为
的函数,故其欧拉方程为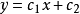 ,由边界条件得
,由边界条件得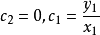 ,于是极值曲线为
,于是极值曲线为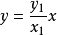 ,相应的极值曲线场为
,相应的极值曲线场为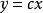 。此时,勒让德强条件为
。此时,勒让德强条件为
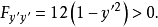
若使勒让德条件成立,应有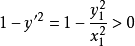 ,即只有当
,即只有当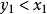 时,极值曲线才能包含在
时,极值曲线才能包含在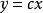 的极值曲线场中2。
的极值曲线场中2。
本词条内容贡献者为:
孙和军 - 副教授 - 南京理工大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国