[科普中国]-正合同伦序列

概念

正合同伦序列是同伦的重要性质之一。联系(绝对)同伦与相对同伦的一种关系。设(X，A，x0)是有基点的空间偶，则有自然的连续映射π：P(X;x0，A)→(A，x0)，从而得到一个映射：

πn-1(π)： πn-1(P(X;x0，A))→πn-1(A，x0)，

用∂记这个映射，即有：

∂： πn-1(P(X;x0，A))=πn(X，A，x0)→πn-1(A，x0).

类似地，可以定义映射：

j*： πn(X，x0)→πn(X，A，x0)，

i*： πn(A，x0)→πn(X，A，x0)，

它们分别是由包含映射：

j： (X，φ，x0)→(X，A，x0)，

i： (A，φ，x0)→(X，A，x0)

诱导的映射。这些集合及映射有如下关系定理：对于带有基点的空间偶(X，A，x0)，下列序列是正合的：

…→πn+1(X，A，x0)→πn(A，x0)→πn(X，x0)→πn(X，A，x0)→…→π1(X，A，x0)→π0(A，x0)→π0(X，x0).

此定理中的序列称为空间偶(X，A，x0)的正合同伦序列。正合同伦序列还有几种其他形式的变体，例如：映射的正合同伦序列、空间三元组(triple)的正合同伦序列等。

同伦设f、g是拓扑空间X到Y的两个连续映射，若存在连续映射H：X×I→Y使得：

H(x，0)=f(x)

H(x，1)=gx∈X

则称f与g同伦，记为f≃g：X→Y或f≃g，映射H称为f与g之间的一个同伦。f与g的同伦H也可理解为单参数映射族{ht}t∈I，ht连续地依赖于t且h0=f，h1=g，即当参数t从0变到1时，映射f连续地形变为g。与常值映射同伦的映射称为零伦的。若以C[X，Y]表示X到Y的一切连续映射之集，则同伦关系≃是C[X，Y]上等价关系，每个等价类称为一个同伦类，同伦类的全体所成集记为[X，Y]。设Y是R的子空间，f，g：X→Y是连续映射，若对每个x∈X，点f(x)与g(x)可由Y中线段连结，则f≃g：X→Y，若Y是R中凸集，任何映射f：X→Y都零伦，即[X，Y]仅含一个元素。设X，Y与Z均为拓扑空间，若f≃f：X→Y，g≃g： Y→Z，则gf≃gf： X→Z。

设X，Y为拓扑空间，若存在连续映射f：X→Y和g：Y→X，使得gf≃Idx且f·g≃idr。这Id、id均表示恒同映射，则称f为同伦等价，g为f的同伦逆，而将X与Y称为具有相同的伦型，或简称同伦的，记作X≃Y。与单点空间同伦的空间称为可缩的，或者存在x0∈X，使得常值映射C：X→X。x1→x0与映射idx同伦，空间X可缩。R和R中凸集均为可缩空间。同伦关系是拓扑空间之间的等价关系。X可缩等价于下列几条中任意一条：(1)idx≃0，即恒同映射idx零伦。(2) 对任意空间Y，映射f：X→Y，有f≃0。(3)对任意空间Z和连续映射g：Z→X，g≃0。

设A是空间X的子空间，i：A→X表包含映射，若存在连续映射r：X→A，使得r|A=idA(或r·i=idA)，则r称为X到A的保核收缩，A称为X的收缩核。若有保核收缩r：X→A满足i·ridx：X→X，则H称为X到A的形变收缩，A称为X的形变收缩核，若同伦H还满足对任意x∈A和t∈I有H(x，t)=x，则H称为X到A的一个强形变收缩，A称为X的强形变收缩核。强形变收缩是形变收缩，且若A是X的形变收缩核，则内射i：A→X是同伦等价。

两个拓扑空间X和Y同伦等价的充要条件是：存在空间Z，使得X与Y分别同胚于Z的两个强形变收缩核。

伦型相同的拓扑空间所共有的性质称为同伦不变量。由于同胚的空间必同伦，故同伦不变量一定是拓扑不变量。代数拓扑学主要研究空间的同伦。

相对同伦相对同伦是同伦群的推广。若(X，A，x0)是有基点的空间偶，定义：

P(X;x0，A)=(X，A，x0)

是X中以x0为始点，终点在A中的所有道路的空间，带有紧开拓扑，则有自然的连续映射π：P(X;x0，A)→A，定义如下：对于ω∈P(X，x0，A)，π(ω)=ω(1).若n≥1是整数，则(X，A，x0)的第n个相对同伦集πn(X，A，x0)定义为：

πn(X，A，x0)=π0(Ω(P(X;x0，A))，ω0)，

其中Ω是定义在有基点的拓扑空间范畴上的闭路函子，π0(Ω(P(X;x0，A))，ω0)是Ω(P(X;x0，A))中包含常值闭路ω0的道路连通分支作为基点的所有道路连通分支的集合。由函子Ω的性质可知，πn(X，A，x0)=πn-1(P(X;x0，A)，ω0)。对于n≥2，πn(X，A，x0)是一个群；对于n≥3，它是一个交换群；对于一切n≥1，πn是定义在有基点的拓扑空间偶上的一个函子。若f：(X，A，x0)→(Y，B，y0)是空间偶之间的保基点连续映射，则记2：

相对同伦有一些与相对同调相类似的性质，例如，相对同伦的正合同伦序列等。

同伦群同伦群(homotopy groups)是基本群的高维推广。基本群是从单位闭区间I到拓扑空间X的闭路的同伦等价类和其运算得到的。考虑n维欧氏空间R中的n维方体：

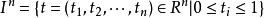
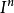是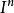的边界，即：

存在i使得，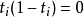

设X为拓扑空间，x0∈X，用Mn(X，x0)表示全体连续映射α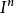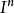：(，)→(X，x0)所成的集合，α和α′相对于I的同伦关系αα′是Mn(X，x0)上的一个等价关系，它把Mn(X，x0)的元素分成一些同伦等价类，用πn(X，x0)表示这些等价类所成的集合.定义映射α*β：(I，I)→(X，x0)，使得：

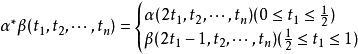
从而，α*β∈Mn(X，x0)，并且，若α∽α′，β∽β′，则：

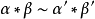
因此，可在πn(X，x0)中定义运算：

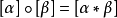并且关于这一运算使它构成群，仍记为πn(X，x0)，称为拓扑空间X的以x0为基点的n维同伦群.1维同伦群就是基本群π1(X，x0).同伦群还有一种等价定义方式，它是用n维球面S代替n维方体I，这种定义给讨论同伦群的性质有时带来方便.类似基本群的讨论，同伦群具有性质：当拓扑空间是道路连通空间时，其同伦群与基点选取无关;利用连续映射诱导的同伦群之间同态的一些性质得出，同伦群是同伦型不变量(更是拓扑不变的)；当n≥2时，同伦群πn(X，x0)是交换群，因而有时把运算写成[α]+[β]。同伦群与同调群的一些基本关系：对于连通复形K的多面体|K|，1维同调群同构于基本群的交换化，即：

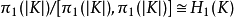这里[π1(|K|)，π1(|K|)]表示基本群π1(|K|)的换位子群。高维同伦群与同调群之间的关系，由赫莱维茨(Hurewicz，W.)的同构定理给出：设|K|是连通复形K的多面体，当n≥2时，若|K|的1，2，…，n-1维同伦群都是平凡群，则πn(|K|)xHn(K)。3