[科普中国]-典型域

第一类典型域

第一种是m行n列的矩阵双曲空间，它是由m行n 列的复元素矩阵Z并且适合于条件

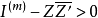的所组成，此处 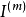表示m行列的单位方阵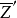， 表示由Z行列互换并取共轭复数所得出的矩阵，因此它是n 行m列的。如果H是一个Hermite 方阵，则以 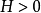表示H是定正的2。

第二类典型域第二种是n 行列的对称方阵的双曲空间，它是由n 行列的复元素对称方阵Z并且适合于条件

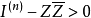的所组成。

第三类典型域第三种是n 行列的斜对称方阵的双曲空间，它是由n 行列的复元素斜对称方阵Z并且适合于条件

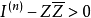的所组成。

第四类典型域第四种可以称为Lie球双曲空间，它是由n(>2)维复元素矢量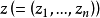 并且适合于诸条件

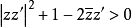及

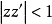的所组成。

相关介绍这四种域的维数(复数维)各为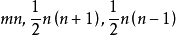 及n。最后一种，也可以表成为 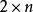实元素矩阵的双曲空间。可递的不可分解的囿对称域仅有六种可能性，除以上的四种之外还有两种，其一是16 维的某一种空间，另一是27维的某一种空间，从维数可以看出这两种域是异常特殊的2。