[科普中国]-纯超越扩张

定义

设E是域F的一个扩域。对于域E的一个子集合S，如果存在一个n元非零多项式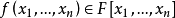 以及S中互不相同的元素 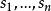使得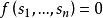 ，那么称S在F上是代数相关的(algebracaly dependent)；否则，称S是代数无关的(algebraically independent)。对于E的一个子集B，如果B在F上是代数无关的且E是F(B) 的代数扩域，那么B称为E在F上的一个超越基(transcendentalbasis)。特别地，如果存在E在F上的一个超越基B使得 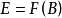，那么称E是F的一个纯超越扩张(purely transcendental extension)。E在F 上的任意两个超越基都有相同的基数，该基数称为E在F上的超越次数(transcendence degree)，记作 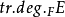。超越次数为1的纯超越扩张称为单超越扩张。

例如，域F上n元有理函数域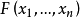 是F的一个纯超越扩域并且超越次数是n。一般地，设E是域F的一个扩域，K是域E的一个扩域，则。

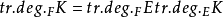设K=ℚ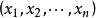 为系数在有理函数域ℚ中的n个变元的有理函数组成的域，因而K是ℚ的一个超越次数为n的纯超越扩张。

超越扩域[transcendental extension feld]

设E是域F的一个扩域。元素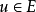 称为F上的超越元(transcendental elenent)。如果u不是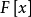中任意非零多项式的根。显然，若 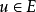是F上的超越元则 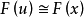。若E中存在一个F上的超越元，则称E为F的一个超越扩张。

设扩域K在F'上的超越基为S，若K=F(S)，则称此域扩张为纯超越扩张，K为F的纯超越扩域。此时，K与F'上一组未定元X的多项式环F[X]的分式域(商域)F'(X)同构，其中X与S的基数相等。一般地，设K是F的任一扩域，若其超越基为S，则F'(S)是F的纯超越扩域，K为F(S)的代数扩域。这样，一个域扩张可分成两种特殊的域扩张来研究。1