[科普中国]-分离函数族

分离函数族(separating family of functions )是一类特殊的函数族。

若D是一个非空实数集合，设有一个对应规则f，使每一个x∈D，都有一个确定的实数y与之对应，则称这个对应规则f为定义在D上的一个函数关系，或称变量y是变量x的函数。一般记作 y=f(x)，x ∈ D。1

概念分离函数族(separating family of functions )是一类特殊的函数族。用C(X)表示拓扑空间X上的所有连续实值函数的全体，F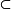C(X)。若对于X的任意相异的两点x，y，存在f∈F使得f(x)≠f(y)，则称F是X上的分离函数族。

等度函数族等度函数族是一类特殊的函数族。设F为拓扑空间X到一致空间(Y，V)的映射族，x∈X.若对于任意V∈V，存在x的邻域U，使得对于任意：

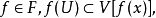则称F在x是等度连续的。若F在X的每点都是等度连续的，则称F是等度连续函数族。若F是等度连续函数族，则F上的点态收敛拓扑是联合连续的。若F关于联合连续拓扑为紧的，则F是等度连续的。2

拓扑空间欧几里得空间的一种推广。给定任意一个集，在它的每一个点赋予一种确定的邻域结构便构成一个拓扑空间。拓扑空间是一种抽象空间，这种抽象空间最早由法国数学家弗雷歇于1906年开始研究。1913年他考虑用邻域定义空间，1914年德国数学家豪斯多夫给出正式定义。豪斯多夫把拓扑空间定义为一个集合，并使用了“邻域”概念，根据这一概念建立了抽象空间的完整理论，后人称他建立的这种拓扑空间为豪斯多夫空间(即现在的T2拓扑空间)。同时期的匈牙利数学家里斯还从导集出发定义了拓扑空间。20世纪20年代，原苏联莫斯科学派的数学家П.С.亚里山德罗夫与乌雷松等人对紧与列紧空间理论进行了系统研究，并在距离化问题上有重要贡献。1930年该学派的吉洪诺夫证明了紧空间的积空间的紧性，他还引进了拓扑空间的无穷乘积(吉洪诺夫乘积)和完全正规空间(吉洪诺夫空间)的概念。

20世纪30年代后，法国数学家又在拓扑空间方面做出新贡献。1937年布尔巴基学派的主要成员H.嘉当引入“滤子”、“超滤”等重要概念，使得“收敛”的更本质的属性显示出来。韦伊提出一致性结构的概念，推广了距离空间，还于1940年出版了《拓扑群的积分及其应用》一书。1944年迪厄多内引进双紧致空间，提出仿紧空间是紧空间的一种推广。1945年弗雷歇又提出抽象距的概念，他的学生们进行了完整的研究。布尔巴基学派的《一般拓扑学》亦对拓扑空间理论进行了补充和总结。

此外，美国数学家斯通研究了剖分空间的可度量性，1948年证明了度量空间是仿紧的等结果。捷克数学家切赫建立起紧致空间的包络理论，为一般拓扑学提供了有力工具。他的著作《拓扑空间论》于1960年出版。近几十年来拓扑空间理论仍在继续发展，不断取得新的成果。

一致空间一致空间是集合上的一种结构。设X为集合，U为X×X的非空子集族。若U满足下列条件，则称U是X上的一致结构：

1.U的每一个元包含对角线Δ。

2.若U∈U，则U-1∈U，其中U-1={(x，y)|(y，x)∈U}。

3.若U∈U，则存在V∈U使得V°V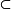U，其中：

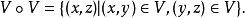4.若U，V∈U，则U∩V∈U。

5.若U∈U并且UVX×X，则V∈U。

具有一致结构U的集合X称为一致空间，记为(X，U)。一致空间的概念是韦伊(Weil，A.)于1938年引入的。布尔巴基(Bourbaki，N.)于1940年首先给予系统的论述。图基(Tukey，J.W.)于1940年用覆盖族定义并研究了一致空间的等价的概念。艾斯贝尔(Isbell，J.R.)于1964年出版的书中，包含了用覆盖叙述的一致空间理论的重要发展。一致空间也可用伪度量族来描述，它是由布尔巴基于1948年给出的。3

本词条内容贡献者为:

王海侠 - 副教授 - 南京理工大学