[科普中国]-局部道路连通空间

局部道路连通空间是一类拓扑空间。设X为拓扑空间，若对于任意x∈X和x的任意邻域U，存在x的一个道路连通的邻域V使得V包含于U，则称X为局部道路连通空间。

简介定义设X为拓扑空间，对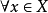 ，如果X在x处是局部道路连通的，则称X为局部道路连通空间。1

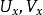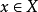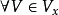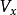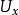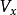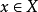相关定义（1）设X为拓扑空间， 分别为 的邻域系与邻域基，如果对 ，V是X的道路连通子集，则称 为 的道路连通邻域基，简称 为 的道路连通邻域基。

（2）设X为拓扑空间，如果对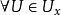 ，V是X的道路连通子集，存在 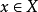的道路连通邻域V，使得 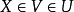，则称X在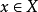 处是局部道路连通的。2

推论（1）拓扑空间X在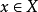 是局部道路连通的当且仅当X在 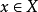处存在道路连通邻域基。

（2）X是局部道路连通空间当且仅当对 ，都存在x的道路连通邻域基。

证明：根据上述定义及推论，拓扑空间x是局部道路连通空间等价于对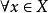 ，X在x处是局部道路连通的。等价于 对 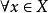，存在x的道路连通邻域基。

（3）实数空间R是局部道路连通空间。

证明：对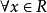 ，则x的所有球形邻域构成的集族 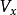为x的邻域 基。又因为R中的球形邻域都是道路连通的 开区间，所以 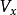为x的道路连通邻域基。由上述定义和推论得，R为局部道路连通空间。

（4）局部道路连通空间必为局部连通空间。

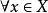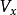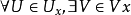证明：设x是局部道路连通空间，由上述定 义和推论得，对 ，存在x的道路连通邻域基 ，使得对 ，满足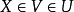 ，因为v是道路连通的，因而也是连通的，所以 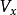是 x 的连通邻域基，因此X是局部连通空间。

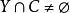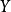（5）设C是拓扑空间x的一个道路连通分支，Y为x的道路连通子集，并且 ，则 包含于C。

证明：因为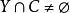 ，故任取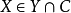 ，对任意y∈Y， 由于Y是X的道路连通子集，而x,y∈Y，所以x与 y是道路连通的，因而x与y属于x的同一个道路连通分支，又x∈C，C是x的道路连通分支，从而y∈C，所以Y包含于C。

（6）道路连通分支是拓扑空间中最大的道路连通子集。

（7）设X为拓扑空间，Q为X的基，如果Q中每个成员都是道路连通，则称Q为X的道路连通基。

（8）设X为拓扑空间，则下列条件等价：

X 是局部道路连通空间；

X 任意开集的任意道路连通分支都是开集；

X 有一个道路连通基；

对所有的x∈X，存在 x 的道路连通邻域基。

（9）局部道路连通空间的每一个道路连通分支都是开集。

（10）设X为局部道路连通空 间，Y为拓扑空间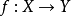， 为连续满的开映射,则Y是局部道路连通空间。

（11）局部道路连通性是拓扑不变性质。

（12）局部道路连通性是有限可积性质。

（13）n维欧氏空间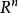 是局部道路连通空间。

（14）局部道路连通空间的每一个开子空间都是局部道路连通空间。

证明：设X是局部道路连通空间，U为X的任意开集，V为U的任意开子集，则V也是X的开集，由定理，V的每一个道路连通分支都是X的开集，故V的每一个道路连通分支也是V的一个开集，从而V的每个道路连通分支也是U 的一个开集，U是X的局部道路连通开子空间。

（15）局部道路连通性对开子空间是可遗传的。

（16）设X是局部道路连通空间，则X是连通空间当且仅当X是道路连通空间，并且X只有一个连通分支，也是它的道路连通分支，此分支为X。

证明：设X是局部道路连通空间，由于X是自身的开子集，根据定理，x是连通空间等价于X是道路连通空间， X为连通空间只有一个道路连通 支，这个道 路连通分支也是X的连通分支，即此分支为X，连通空间与道路连通 空间，局部连通空间与局部道路连通空间，连通分支与道路连通分支以及n维欧氏空间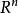 之间的关系框图如下：

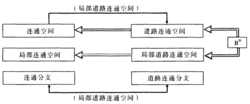
相关概念连通空间设X是一个拓扑空间。如果X中有两个非空的隔离子集A和B，使得X= A∪ B，则称X是一个不连通空间；否则，则称X是一个连通空间。

局部连通空间设X是一个拓扑空间。如果x∈ X的每一个邻域中都包含着x的某一个连通的邻域V，则称拓扑空间在点x处是局部连通的。如果拓扑空间X在它的每一个点处都是局部连通的，则称是一个局部连通空间。

局部连通的拓扑空间也不必是连通的。例如，每一个离散空间都是局部连通空间，但包含着多于一个点的离散空间却不是连通空间。又例如，n维欧氏空间的任何一个开子空间都是局部连通的(这是因为每一个球形邻域都同胚于整个欧氏空间，因而是连通的)，特别地，欧氏空间本身是局部连通的。另一方面，欧氏空间中由两个无交的非空开集的并作为子空间就一定不是连通的。

此外根据定义立即可见：拓扑空间X在点x∈X处是局部连通的当且仅当x的所有连通邻域构成点二处的一个邻域基。3

道路连通空间设X是一个拓扑空间，如果对于任何x, y，存在着X中的一条从x到y的道路(或曲线)，我们则称X是一个道路连通空间。X中的一个子集Y称为X中的一个道路连通子集，如果它作为X的子空间是一个道路连通空间。

实数空间R是道路连通的，这是因为如果x, y∈R，则连续映射f： [0,1] R定义为对于任何t∈[0,1]有f(t)=x+t(y-x)，便是R中的一条以x为起点以y为终点的道路。也容易验证任何一个区间都是道路连通的。4

本词条内容贡献者为:

胡启洲 - 副教授 - 南京理工大学