[科普中国]-射影变形

概念

射影变形(projective deformation)是射影曲面论的重要概念之一。富比尼拓广普通曲面变形到射影曲面论而导入的概念。设曲面S和S′之间存在点对应，且对于S任意点P均可找到直射T，变换P到S′的对应点P′，S上过P的任意曲线Γ变换到Γ-，Γ-和Γ的对应曲线Γ′在点P′构成二阶解析接触，则称S和S′为互为射影变形的曲面，它们的对应称为射影变形。两曲面互为射影变形的充分必要条件是它们的渐近曲线互相对应且在对应点的β，γ分别相等，或者两曲面在对应点有相同的射影线素。

射影线素射影线素是射影曲面论的重要概念之一。欧氏线素在射影曲面论的推广，用交比表达。设u，v是曲面S的参数，x是S的点P(x)的齐次坐标。若ξ=ρ(x xuxv)，其中ρ是非零因子，(x xuxv)是行列式(X x xuxv)关于第一列四个元的代数余子式。定义分式：

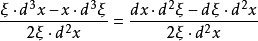
为S的射影线素。这个定义最初由德拉齐尼(Terracini，A.)于1926年给出。若取u，v为渐近参数，则射影线素为：

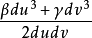
称为富比尼线素。

射影微分几何学微分几何学的一个分支，从属于射影变换群。其思想来源于C.F.克莱因1872年的著名演说“埃朗根纲领”，在那里将几何学归结为可逆变换群的几何不变量理论加以分类。研究的对象主要是曲线、曲面、共轭网等在射影变换群下的不变量、协变图形及其性质。19世纪末，法国数学家达布在《曲面通论教程》(1887—1896) 和《正交系与曲线坐标》(1898)中系统介绍了近百年来曲线和曲面微分几何学方面的成就，其中蕴含了射影微分几何学的萌芽。同时代的数学家阿尔方也对射影微分几何做过系统研究。1906年德国—美国数学家维尔钦斯基发表论著《曲线和直纹曲面的射影微分几何》，将曲线的射影微分几何理论推广到曲面上，成为现代射影微分几何的创始人之一。其后意大利数学家富比尼用一种射影不变的方法获得“富比尼规范坐标”，详尽阐述了系统研究曲线和曲面的过程。他与捷克数学家切赫合著的《射影微分几何》(2卷，1926—1927)与《曲面射影微分几何引论》(1931)已成为该学科的经典著作。

1937年法国数学家É.嘉当出版《射影联络空间理论教程》，创立新的活动标架法，重新建立起射影曲面论，振兴了微分几何学。他引入一般纤维丛理论，构造了仿射、射影及保形的广义联络空间，他的外形法为现代高维射影空间共轭网理论提供了依据。此外，意大利数学家邦皮亚尼和中国数学家苏步青都对射影微分几何做过系统的研究工作。苏步青从20世纪30年代末开创并发展起结构式射影微分几何，用几何作图法建立协变的构图和不变量，特别是用平面曲线在某种奇异点的不变量以表达其他几何不变量，这是一项具有代表性的显著成果。他的有关著作有《射影曲线概论》(1954)、《射影曲面概论》(1964)、《射影共轭网概论》(1978)等。2

富比尼意大利数学家。生于威尼斯，卒于美国纽约。早年在比萨高等师范学校攻读数学。先后在卡塔尼亚、热那亚和都灵等地的大学任教，1939年移居美国，任普林斯顿高等研究院教授。富比尼是20世纪初意大利数学界的代表人物，其数学研究涉及微分方程、多复变函数论、群论、射影微分几何学、变分法、积分化简、概率分析等许多领域。他最早使用微分形式研究射影几何，是射影微分几何学的先驱者之一。在群论中，他建立了通过线性群和运动群理论判定连续群的准则。在积分论中，他给出的把高维的勒贝格积分化为累次低维积分的定理(富比尼定理)，至今仍是积分论中最重要的定理之一。他在物理学方面也做出许多贡献。1919年获意大利王室授予的奖金。1928—1937年担任《纯粹与应用数学年刊》编辑。其主要著作有《自守函数不连续群论导引》(1908)、《数学分析讲义》、《射影微分几何》(2卷，1926—1927，与切赫(E. Cech，1893—1960)合作)等。

射影几何亦称投影几何。几何学的一个分支。主要研究图形在射影对应(射影变换)下不变的几何性质。射影变换是射影几何中最重要的几何变换。这种变换的主要特点是保持结合性。例如，点与直线及点与平面的结合性等.交比是射影几何中最基本的不变量，其他不变量都可以用交比表示出来。

射影几何的思想，特别是其中的透视投影原理，早在古罗马时代已为画家所认识和应用;射影几何的基本不变量——交比，早已为帕普斯(Pappus，(A))所熟知;射影几何的一些命题也早已为古代几何学家所得到。然而，射影几何作为几何学的一个独立分支学科却是在19世纪初期，随着几何学的发展以及绘画与建筑的需要而形成和发展起来的。1822年，彭赛列(Poncelet，J.-V.)发表了射影几何的第一部系统著作《论图形的射影性质》一书。他通过几何方法引进无穷远元素，研究了二次曲线和二次曲面的配极理论，并由此导出一般的对偶原理.稍后，施泰纳(Steiner，J.)研究了利用简单图形产生较复杂图形的方法，并于1832年引进了线素二次曲线概念.。1847年，冯·施陶特(von Staudt，K.G.C.)通过几何作图来建立直线上点的坐标，进而使交比与射影坐标不依赖于任何度量.此外，他还以精巧的方法给出虚元素的几何解释。与此同时，运用解析法研究射影几何也有了长足的发展.首先是默比乌斯(Mo¨bius，A.F.)创立了一种齐次坐标，揭示了对偶原理与配极之间的关系，并于1827年对交比的概念给出了完善的处理。接着，普吕克(Plücker，J.)引进了另一种齐次坐标，得到了平面上无穷远线的方程和无穷远圆点的坐标.他还引入了线坐标的概念，于是从代数观点自然就得到对偶原理，并得到一般线曲线的概念。在19世纪前半叶的几何研究中，综合法与解析法的争论非常激烈.一些几何学家坚持运用综合法，如彭赛列、施泰纳等。综合法也确实有它独特的优点，它形象鲜明，使有些问题的论证直接而简洁.由于他们的努力，使综合射影几何形成了一个优美的体系.1882年，帕施(Pasch，M.)建立了第一个射影几何演绎体系.1872年，克莱因(Klein，(C.)F.)利用变换群的观点把各种几何学联系起来，他在埃尔朗根纲领中提出了这个观点，并把几种经典几何看做是射影几何的子几何，使这些几何之间的关系变得更加明朗。3