[科普中国]-带积范畴

概念

带积范畴(category with product)是环上模范畴、有限生成投射模范畴等重要范畴关于直和及(交换环的情况下)张量积性质的抽象与概括。设C为一个范畴，它有零对象0(即Hom(0，A)与Hom(A，0)都只有一个元素，A∈C)。若⊥：C×C→C为一个函子且满足A⊥00⊥AA；A⊥BB⊥A；A⊥(B⊥C)(A⊥B)⊥C(这些同构都是自然的)，A，B，C∈C，则称⊥为积函子，(C，⊥)称为带积范畴。例如，环R上模范畴对⊕是带积范畴，R上的有限生成投射模范畴对⊕也是带积范畴。当R可换时，它们关于(张量积)也是带积范畴。R上的可逆模的同构类范畴Pic R关于也是带积范畴。对带积范畴C可与环上关于有限生成投射模范畴同样地定义其K0群。即以〈A〉表A∈C的同构类，以{〈A〉|A∈C}为基得自由阿贝尔群F，记由一切〈A⊥B〉-〈A〉-〈B〉生成的子群为R。定义K0(C，⊥)=F/R。这种定义更具一般性且可用于其他学科如代数几何、 纤维丛理论等。

范畴范畴是范畴论的基本概念之一。称C是一个范畴，是指C满足下述六点：

1.C有一个对象类{A，B，C，…}(不要求它是一个集合，即不要求它满足集合论的公理，只要求能判别出是不是它的对象)，常记为ObjC或简记C。

2.对C的任两对象A，B，有一个确定的集合(可为空集)Hom(A，B)，其元素称为由A到B的态射，记为f∈Hom(A，B)或f：A→B。

3.对给定的f∈Hom(A，B)与g∈Hom(B，C)有惟一的gf∈Hom(A，C)，称为f与g的合成。

4.Hom(A，B)与Hom(C，D)有公共元是指A=C且B=D.。

5.态射合成满足结合律。

6.对C的任意对象A，Hom(A，A)至少有一个元素εA使对σ∈Hom(A，B)恒有σεA=σ=εBσ，称εA为A的恒等态射(εB为B的恒等态射).

例如，以一切集合作对象，以集合映射作态射，则得集合范畴Set(简称集范畴).以一切拓扑空间作对象，以连续映射作态射，则得拓扑空间范畴Top。以一切环为对象，以环同态作为态射得环范畴Ring。类似地，可得群范畴Group，阿贝尔群范畴AG，环R上的左R模范畴RM等。以自然数为对象，a|b(表示a整除b)时定义Hom(a，b)有惟一元素φab，ab时定义Hom(a，b)=(空集)，也得到一个范畴。一般地，对每个拟序集都可仿此定义范畴。2

环环是对并与差运算封闭的集类，测度论中重要概念之一。设F是Ω上的一个非空集类。如果它对集的并及差运算封闭，即对任何A，B∈F，都有A∪B∈F，A\B∈F，则称F为Ω上的环。例如，若F是由实直线R上任意有限个左开右闭的有限区间的并集

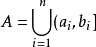
的全体构成的集类，则F是R上的一个环.环也是对于交与对称差运算封闭的集类，并按这两种运算成为布尔环。要把R上的勒贝格测度和勒贝格-斯蒂尔杰斯测度以及相应的积分理论推广到更一般的集合上，就需要做一系列奠基工作，其中之一是建立一些特殊的集类并研究其性质。环以及半环、σ环、代数、σ代数等重要集类正是为了这一目的而引入的。

模模是一个重要的代数系统。它是一个带算子区A的交换(加)群M。给定集合A与交换群M，若定义了a∈A与x∈M的乘积ax∈M，并且这个积满足条件：

1.a(x+y)=ax+ay (a∈A，x，y∈M)，

则称A为M的算子区，称M为带算子区A的模，又称为A上的模或A模.这时，由对应(a，x)→ax确定的映射A×M→M，称为A作用到M上的运算.任意a∈A可诱导出M的自同态aM：x→ax，而考虑交换群M能否成为A模就是看能否给出映射

μ： A→End(M)， a→aM.

特别地，考虑A是结合环，若满足上述条件1的A模还满足：

2.(a+b)x=ax+bx;

3.(ab)x=a(bx);

即映射μ：A→End(M)为环同态，则称M为左A模或左环模.由于A到M上的运算是写在左侧，所以M就称为左A模，记为AM.类似地，有右A模M，记为MA.若A有单位元1，且又满足条件

4.1x=x (x∈M);

则称M为酉模或幺模，以下设A模都是酉模。

模范畴模范畴是一种重要的范畴。指所有以模和模之间的同态组成的范畴。利用范畴的观点来讨论模和环是一种重要方法。若A是环，则所有的左A模组成的类和所有左A模M，N之间的模同态HomA(M，N)，以及模的同态的乘法运算法则构成一个范畴，称为左A模范畴，记为：A-Mod。3