[科普中国]-双正则理想

双正则理想(biregular ideal)是一类特殊理想。若环R中元素a所生成的主理想有单位，则a称为R的双正则元。环R的一个理想称为双正则理想，是指该理想中每个非零元都是双正则元。双正则理想是双正则环。

概念双正则理想(biregular ideal)是一类特殊理想。若环R中元素a所生成的主理想有单位，则a称为R的双正则元。环R的一个理想称为双正则理想，是指该理想中每个非零元都是双正则元。双正则理想是双正则环。若A是R的双正则理想，B是A的双正则理想，则B是R的双正则理想。环R的双正则理想的和也是双正则的，且R含惟一极大双正则理想，记为B(R)。但至今不知，R/B(R)是否不含双正则理想。1

理想理想是集合论中的基本概念之一。设S为任意集合，若I⊆P(S)且满足：

1.∅∈I；

2.若X，Y∈I，则X∪Y∈I；

3.若X，Y⊆S，X∈I，Y⊆X，则Y∈I；

则称I为集合S上的理想。理想的概念在现代数学的几乎每个分支中均有应用，且有许多变体或引申。例如，布尔代数上的理想即为集合上的理想的一种变体。设B为任意布尔代数，若B的一个子集I满足：

1.0∈I，1∉I(其中0，1分别为布尔代数B中的零元与么元)；

2.对任何u∈I，v∈I，有u+v∈I；

3.对任何u，v∈B，若u∈I且v≤u，又v∈I；

则称I为B上的理想。理想与滤子有非常密切的联系。1

环环是对并与差运算封闭的集类，测度论中重要概念之一。设F是Ω上的一个非空集类.如果它对集的并及差运算封闭，即对任何A，B∈F，都有A∪B∈F，A\B∈F，则称F为Ω上的环。例如，若F是由实直线R上任意有限个左开右闭的有限区间的并集：

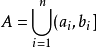的全体构成的集类，则F是R上的一个环.环也是对于交与对称差运算封闭的集类，并按这两种运算成为布尔环。要把R上的勒贝格测度和勒贝格-斯蒂尔杰斯测度以及相应的积分理论推广到更一般的集合上，就需要做一系列奠基工作，其中之一是建立一些特殊的集类并研究其性质、环以及半环、σ环、代数、σ代数等重要集类正是为了这一目的而引入的。

右拟正则理想右拟正则理想是一类重要的理想。元素的拟正则性是元素幂零性的自然推广，是从元素刻画雅各布森根而引入的概念。对环R的一个元a而言，若存在R中元b使得a+b+ab=0(a+b+ba=0)，则称a为R的右(左)拟正则元，b为a的右(左)拟逆元。环R的一个理想A，若A中每个元都是右(左)拟正则元，则称A为右(左)拟正则理想。环R的一个右理想称为右拟正则右理想，若它的每个元皆为右拟正则元。同样地，可定义左拟正则左理想。任何诣零左(右)理想是左(右)拟正则左(右)理想。有些文献采用a+b-ab=0(a+b-ba=0)来定义拟正则元。

集合论数理逻辑四个主要分支之一，是关于无穷集合和超穷数的数学理论。数学里遇到的无穷有： 无穷过程、无穷小和无穷大。必须能作数学的处理，能进行运算，这样的无穷才能算作数学的对象。一般说来，集合就是我们把直观上或思想上的一些确定的彼此不同的对象作为一个整体。组成某一集合的事物(或对象)叫做该集合的元素，用逻辑的话来说就是概念外延相同的全类。构成集合的元素个数为有限时称为有限集。若构成集合的元素个数为无限多时称为无限集。德国逻辑学家康托尔于1972年建立。集合论对数学的发展产生了巨大的影响，今天已成为数学各个分支不可缺少的基础和工具。同时也渗透到数理逻辑的各个分支。1

本词条内容贡献者为:

王海侠 - 副教授 - 南京理工大学