[科普中国]-皮卡概形

简介

皮卡概形是光滑代数簇X的皮卡簇𝕭(X)的概念在概形理论框架内的自然推广。

为了对任意的S概形X定义皮卡概形。先要考虑概形S上的概形的范畴Sch/S里的相对皮卡函子（relative Picard functor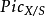）。这个函子在S概形S'上的值是一个群

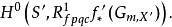
这里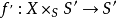是基变换态射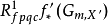，是在严格平坦拟紧态射的格罗滕迪克拓扑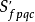里与预层

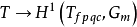相关联的层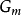，表示标准的乘法群层。如果皮卡函子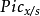是在Sch/S上可表示的，则表示它的 S 概形被称为 S 概形的相对皮卡概形（relative Picard scheme），记为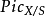。如果 X 是某个域 k 上的代数概形，k有一个有理k点，则对任意 k 概形 S'有

特别地，X/k(k)=Pic(X)可被等同于的 k 有理点的群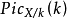（如果这个群存在的话）。1

性质如果f ：X → S是具有几何整纤维的射影态射，则概形存在而且是局部有限可表示的可分群S概形。

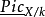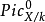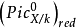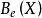如果S=Spec(k)，则的单位连通分支是一个代数 k 概形，而且对应的约化 k 概形正式皮卡簇。概形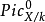的局部环里的幂零元给出了皮卡概形的许多附加的信息，而且能解释在特征数 p>0 的域上的代数几何里的各种“病态”。另一方面，在特征数0定域上概形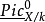总是约化的。当 F 是光滑代数曲面且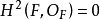时已经知道是一种约化概形。

对任何有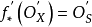的真平坦态射f ：X → S（当基S为诺特时，它是有限可表示的），函子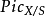对于任何基变换态射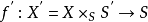是 S 上的代数空间。特别地，当基域 S 是局部阿廷环的谱时，函子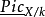是可表示的。