简介
若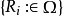 为
为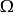 上的一个半环正向系,有半环R,对每个
上的一个半环正向系,有半环R,对每个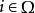 ,有半环态射
,有半环态射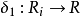 满足:
满足:
(1)对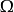 中所有的i≤j 有
中所有的i≤j 有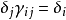 ;
;
(2)若任意半环S和态射集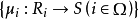 对于
对于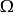 中所有i ≤j 满足:
中所有i ≤j 满足: ,则存在唯一的半环态射η:R →S 对所有的
,则存在唯一的半环态射η:R →S 对所有的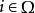 有
有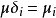 。
。
称满足以上条件的 是正向极限,记为:lim Ri 。1
是正向极限,记为:lim Ri 。1
正向极限存在性若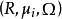 是一个半环正向系,S 是Ri的无交并,在S上定义二元关系
是一个半环正向系,S 是Ri的无交并,在S上定义二元关系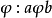 等价于
等价于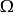 中存在i , j ≤k 使得a ∈Ri,b∈Rj,μik(a)=μjk(b)。显然对所有的n≥k 有μin(a)=μjn(b)。
中存在i , j ≤k 使得a ∈Ri,b∈Rj,μik(a)=μjk(b)。显然对所有的n≥k 有μin(a)=μjn(b)。
令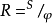 ,半环态射
,半环态射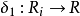 ,则
,则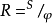 是半环正向系
是半环正向系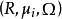 的正向极限。
的正向极限。
正向极限的一些性质(1)半环S上的元素a称为加法(乘法)幂等的,如果它满足附加条件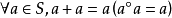 ,半环 S 称为幂等的。
,半环 S 称为幂等的。
(2)半环 S 称为单半环,若 r ∈S ,a +1 =1;半环 S 称为零和自由的。如果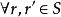 ,有r+r'=0,则r+r'=0;半环 S 称为整的,如果
,有r+r'=0,则r+r'=0;半环 S 称为整的,如果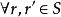 ,有
,有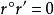 ,则r=0或者r'=0。
,则r=0或者r'=0。
(3)若 R 是半环正向系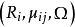 的正向极限,其半环态射
的正向极限,其半环态射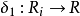 ,则 R 是加法(乘法)幂等的当且仅当对
,则 R 是加法(乘法)幂等的当且仅当对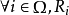 是加法(乘法)幂等的.
是加法(乘法)幂等的.
(4)若 R 是半环正向系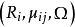 的正向极限,其半环态射
的正向极限,其半环态射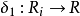 ,则对
,则对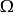 中所有i≤j,
中所有i≤j,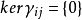 ,当且仅当
,当且仅当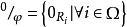 。
。
(5)若 R 是半环正向系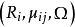 的正向极限,其半环态射
的正向极限,其半环态射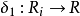 ,且
,且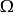 中所有i≤j,
中所有i≤j,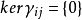 ,则:
,则:
Ri(i ∈ Ψ)是零和自由的当且仅当 R 是零和自由的;
Ri(i ∈ Ψ)是整的当且仅当 R 是整的。
(6)若 R 是半环正向系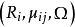 的正向极限,其半环态射
的正向极限,其半环态射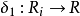 ,若
,若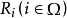 是单的,则R是单的,如果
是单的,则R是单的,如果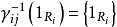 ,那么反之也成立。
,那么反之也成立。
(7)若 R 是半环正向系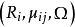 的正向极限,其半环态射
的正向极限,其半环态射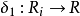 ,若
,若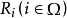 是环,则R是环。
是环,则R是环。
(8)若 R 是半环正向系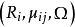 的正向极限,其半环态射
的正向极限,其半环态射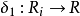 ,若
,若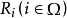 是加法幂等的,
是加法幂等的,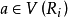 ,则
,则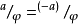 当且仅当
当且仅当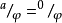 。
。
(9)设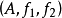 为
为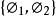 的推出,则A必是半正环正向系
的推出,则A必是半正环正向系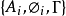 的正向极限,其中
的正向极限,其中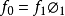 。23
。23
反向极限反向极限(inverse limit)亦称逆向极限或上极限。它是积与拉回概念的推广,也是正向极限的对偶概念,在范畴论、同调代数、代数K理论、代数几何等学科中有重要应用.设矛为一个范畴,了为一个拟序集所成的范畴。省的一个带指标集了的反向系是指一个反变函子F。
正向极限的等价刻画第一定义设是一个范畴,I,J,L是指标集,集合I与集合J元素之间有关系“≤”。集合I与集合L元素之间有关系“≤”,满足对任意J∈J,存在i∈I,使得i≤j;对任意l∈L,存在i∈I,使得i≤l;对任意i∈I,存在J∈J,l∈L,使得i≤j,i≤l。
且若i≤j,有有确定的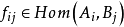 ;若i≤l,有确定的
;若i≤l,有确定的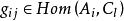 ,称交换图族为广义推出族。
,称交换图族为广义推出族。
第二定义设A是一个范畴,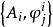 为范畴A中的一个以l为指标集的正向系,若
为范畴A中的一个以l为指标集的正向系,若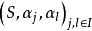 是
是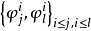 的广义推出,则称
的广义推出,则称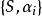 为正向系
为正向系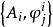 的正向极限。
的正向极限。
正向化限的第二定义与第一定义是等价的。




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国