在数学的一个抽象分支范畴论中,范畴的等价(equivalence of categories)是两个范畴间的一个关系,在这种关系之下的范畴是“本质上一样的”。从数学的许多地方都有范畴等价的例子。建立一个等价涉及展示所考虑的数学结构间很强的相似性。
如果一个范畴等价于另一个范畴的反范畴,则我们说“范畴的对偶性”,以及这两个范畴对偶等价。范畴的等价由所涉范畴的一个函子组成,这个函子要求有一个“逆”函子。但与通常代数语境的同构不同,这个函子与它的逆不必是恒等映射,二只要每个对象自然同构与在此符合函子下的像。从而我们可以说这个函子是差一个同构下的逆。这实际上是范畴的同构的概念,其中要求逆函子的严格性质,但这比“等价”概念用得要少。1
定义正式定义为,给定两个范畴C与D,一个范畴等价包括函子F:C→D,函子G:D→C,以及两个自然同构 ε:FG→ID与 η:IC→GF。这里FG:D→D与GF:C→C分别为F与G的复合,而IC:C→C与ID:D→D分别为C与D的恒同函子。如果F与G是反变函子我们则说范畴的对偶。
通常我们不指出如上所有数据。例如,我们说范畴C与D是等价的(对偶等价)如果它们之间存在一个等价(对偶等价)。进一步,我们说F是一个范畴的等价如果如上逆函子G以及自然同构存在。但要注意F所具有的信息不足以构造G以及自然同构:存在许多不同的选择(见下面的例子)。2
等价的刻画可以证明函子F:C→D给出范畴的等价当且仅当它是:
完全,即给定C的任何两个对象c1与c2,由F给出的映射 HomC(c1,c2) → HomD(Fc1,Fc2) 是满射。
忠实,即对C的任何两个对象c1与c2,由F给出的映射 HomC(c1,c2) → HomD(Fc1,Fc2) 是单射;
本质满,即D中每个对象d同构与某个形如Fc的对象。
这是一个相当有效和常用的判别法,因为不必真正构造出逆G以及FG,G'与恒同函子之间的自然同构。另一方面,尽管上面性质保证了范畴等价的存在性(假定背景集合论具有一个足够强的选择公理),缺少的数据没有完全确定,通常有许多选择。只要可能,给出缺少的构造是个好主意。正因为如此,具有这些性质的函子有时叫做范畴的弱等价(不幸地是这个术语与同伦论冲突)。
它与伴随函子概念也有紧密联系。如下论断对函子F:C→D与G:D→C等价:
存在从FG到ID与从IC到GF的自然同构,分别叫做余单位与单位。
F是G的一个左伴随且两个函子都完全且忠实。
F是G的一个右伴随且两个函子都完全且忠实。
从而我们可以将两个函子之间的伴随关系视为“非常弱的等价”。假设伴随的自然变化已经给定,所有这些确保了一个明确的构造,且不需要选择原理。关键性质是需要证明伴随的余单位是同构当且仅当右伴随是完全且忠实的函子。3
例子考虑范畴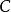 只有一个对象
只有一个对象 以及一个态射
以及一个态射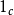 ,以及范畴
,以及范畴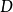 具有两个对象
具有两个对象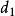 ,
,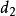 以及四个态射:两个恒同态射
以及四个态射:两个恒同态射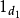 ,
,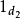 以及两个态射
以及两个态射 与
与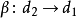 。范畴
。范畴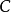 与
与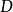 是等价的;我们可以(权为一例)构造
是等价的;我们可以(权为一例)构造 将
将 映为
映为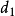 与
与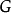 将
将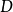 的两个对象映为
的两个对象映为 以及所有态射映为
以及所有态射映为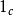 。
。
相比之下,只有一个对象与一个态射的范畴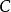 与具有两个对象与两个恒同态射从而这两个对象不同构的范畴
与具有两个对象与两个恒同态射从而这两个对象不同构的范畴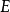 不等价。
不等价。
考虑一个范畴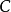 ,有一个对象
,有一个对象 ,以及两个态射
,以及两个态射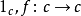 。令
。令 为
为 的恒同映射,设
的恒同映射,设 。当然
。当然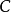 等价于自己,在所有需要自然同构的地方可以取
等价于自己,在所有需要自然同构的地方可以取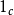 ,便给出函子
,便给出函子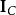 与自己自然同构。但是
与自己自然同构。但是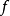 同样给出
同样给出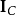 到自己的一个自然同构,尽管恒同函子是一个范畴同构,在这个例子中我们仍然可以选取每个方向的自然同构。
到自己的一个自然同构,尽管恒同函子是一个范畴同构,在这个例子中我们仍然可以选取每个方向的自然同构。
考虑有限维实向量空间范畴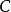 ,以及所有实矩阵范畴
,以及所有实矩阵范畴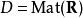 (后一二范畴在可加范畴中有解释)。则
(后一二范畴在可加范畴中有解释)。则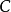 与
与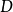 是等价的:函子
是等价的:函子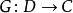 将
将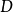 中每个对象
中每个对象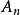 映为向量空间
映为向量空间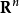 ,而
,而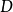 中矩阵到对应线性映射是完全、忠实且本质满的。
中矩阵到对应线性映射是完全、忠实且本质满的。
代数几何的中心论题是仿射概形与交换环的对偶性。函子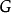 将每个交换环映射它的谱,概形定义为此环的主理想。其伴随
将每个交换环映射它的谱,概形定义为此环的主理想。其伴随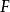 将每个仿射概形映为它的环的整体截面。
将每个仿射概形映为它的环的整体截面。
在泛函分析中,有单位的交换C*-代数反变等价于紧豪斯多夫空间范畴。在这个对偶下,每个紧豪斯多夫空间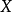 对应于
对应于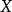 上的连续复值函数代数,而每个交换 C*-代数对应于它的极大理想空间。这就是盖尔范德表示。
上的连续复值函数代数,而每个交换 C*-代数对应于它的极大理想空间。这就是盖尔范德表示。
在格理论中,有不少对偶,基于将某些格类与拓扑空间类联系起来的表示定理。可能最有名的这类定理是布尔代数的斯通表示定理,这是一般概念斯通对偶性的特例。每个布尔代数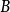 映为
映为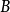 的超滤子集合上的一个特定的拓扑。反之,任何开闭子集上的拓扑给出一个布尔代数。我们得到了布尔代数(与他们的同态)范畴与斯通空间(与光滑映射)。斯通对偶性的另一种情形是伯克霍夫表示定理指出有限偏序与有限分布格之间的对偶性。
的超滤子集合上的一个特定的拓扑。反之,任何开闭子集上的拓扑给出一个布尔代数。我们得到了布尔代数(与他们的同态)范畴与斯通空间(与光滑映射)。斯通对偶性的另一种情形是伯克霍夫表示定理指出有限偏序与有限分布格之间的对偶性。
在无点拓扑学中,空间局部(spatial locale)范畴等价于朴素空间(sober space)的对偶。3
性质大概说来,一个范畴等价保持所有范畴性概念与性质。如果F:C→D是一个等价,则如下论断都成立:
C的对象c是一个始对象(或终对象,或零对象)当且仅当Fc'是D的一个始对象(或终对象,或零对象)当且仅当。
C中态射 α 是单态射(或满态射或同构),当且仅当Fα是D中单态射(或满态射或同构)。
函子H:I→C有极限(或余极限)当且仅当函子FH:I→D有极限(或余极限)Fl。这可以用于等化子、乘积与余乘积,等等。应用于核与余核,我们发现等价F是一个正合函子。
C是一个笛卡儿闭范畴(或一个拓扑斯)当且仅当D是笛卡儿闭(或拓扑斯)。
对偶性将所有概念对换过来:它们将始对象变成终对象,单态射变成满态射,核变成余核,极限变成余极限,等等。
如果F:C→D是一个范畴等价,而G1与G2是两个逆,则G1与G2是自然同构的。
如果F:C→D是一个范畴等价,若C是一个预可加范畴(或可加范畴,或阿贝尔范畴),则D可以变成预可加范畴(或可加范畴,或阿贝尔范畴)并使F成为可加函子。另一方面,可加范畴之间的任何等价必然可加。(注意后一个论断对预可加范畴的等价不成立。)
一个范畴C的自等价是一个等价F:C→C。如果我们将两个自然同构的自等价视为一样的,则C的自等价在复合下构成一个群。这个群抓住了C的本质对称。(注意:如果C不是小范畴,则C的自同构可能是一个真类而不是集合。)3




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国