单位态射(unit morphism)亦称可逆态射,是集合范畴中单位映射(可逆映射)概念的推广。设f:A→B为范畴C中的态射,若有态射u使uf=εA(A上的恒等态射),则称f为左可逆态射,称u为f的左逆态射。若有态射v使fv=εB,则称f为右可逆态射,称v为f的右逆态射。若f同时为左可逆态射与右可逆态射,就称f为单位态射。当f是单位态射时,上述的u=v。因此单位态射又称为等价态射。
定义设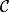 是范畴,
是范畴, ,如有
,如有 ,使得
,使得
 则称
则称 等价(或
等价(或 同构)。满足上述条件的
同构)。满足上述条件的 叫做单位态射(或同构态射)。
叫做单位态射(或同构态射)。
相关概念等价态射等价态射(equivalent morphism)亦称同构态射,它是群论、环论、模论中同构概念的推广,因此也简称同构。在范畴中可用它们将其对象类分成等价类进行研究,因此起着重要的作用,设C为范畴, ,若有
,若有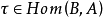 使
使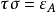 且
且 (ε表恒等态射),则
(ε表恒等态射),则 都称为等价态射且互称为逆态射,此时称对象
都称为等价态射且互称为逆态射,此时称对象 为等价的。等价态射一定是单位态射**,反之亦然**。等价态射之逆是惟一的1。
为等价的。等价态射一定是单位态射**,反之亦然**。等价态射之逆是惟一的1。
单态射单态射是集合范畴 中单射概念的推广,它与满态射是互为对偶的概念。范畴C中的态射
中单射概念的推广,它与满态射是互为对偶的概念。范畴C中的态射 ,若有左可消性质,即对使态射合成有意义的态射
,若有左可消性质,即对使态射合成有意义的态射 ,由
,由 可断定
可断定 ,则称
,则称 为C中的单态射,若
为C中的单态射,若 为单态射,则
为单态射,则 必为单态射;单态射的合成仍为单态射;单位态射必为单态射;甚至左可逆态射也是单态射。
必为单态射;单态射的合成仍为单态射;单位态射必为单态射;甚至左可逆态射也是单态射。
满态射满态射是集合范畴中满射概念的推广,它是单态射的对偶概念。范畴C中的态射 ,若有右可消性质,即由态射合成
,若有右可消性质,即由态射合成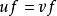 可断定
可断定 ,则称
,则称 为C中的满态射,若
为C中的满态射,若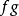 为满态射,则
为满态射,则 为满态射;满态射的合成仍为满态射;**单位态射必是满态射,甚至右可逆态射也是满态射。**在群范畴中满态射即满同态;在环范畴中满同态为满态射,但反之不真。
为满态射;满态射的合成仍为满态射;**单位态射必是满态射,甚至右可逆态射也是满态射。**在群范畴中满态射即满同态;在环范畴中满同态为满态射,但反之不真。
双态射双态射是集合范畴中双射概念的推广,在范畴中同时为单态射与满态射的态射称为双态射。换言之,双态射即满足左可消与右可消的态射,在群范畴与阿贝尔群范畴等范畴中,双态射就是满单同态(同构)。单位态射一定是双态射,但反之一般不真**,在阿贝尔范畴中双态射即单位态射1**。
阿贝尔范畴阿贝尔范畴(Abelian category)是一种特殊的加性范畴,因此具有更丰富的性质。一个加性范畴C称C为阿贝尔范畴,若再满足下述三条件:
1.任何态射f都有核kerf与上核coker f;
2.任何单(满)态射都是其上核(核)的核(上核);
3.任何态射σ都可分解为一个单态射η与一个满态射π的合成σ=ηπ(称为σ的标准分解式)。
阿贝尔群范畴、环R上的R模范畴都是阿贝尔范畴,阿贝尔范畴具有加性范畴的一切性质,阿贝尔范畴的对偶范畴仍为阿贝尔范畴,阿贝尔范畴中既单且满的态射是单位态射,阿贝尔范畴在同调代数及代数几何中都是最常用的一类范畴1。
态射的核态射的核(kernel of a morphism)是群论中同态核概念的推广(不过在群论中同态核是一个正规子群,而在群范畴中则是指此正规子群及其在群中的嵌入同态),态射的核是态射的上核之对偶概念。设范畴C有零对象(因而有零态射0),f∈Hom(A,B),所谓f的核ker f,是指C的一个对象K与一个态射η∈Hom(K,A)组成的对(K,η),它满足:1.η为单态射;2.fη=0;3.对任何g∈Hom(D,A),只要fg=0就必有τ∈Hom(D,K)使ητ=g (条件1可去掉,但在3中须强调“必有惟一的τ”)。
若f的核存在,则在等价意义下是惟一的,有时为强调态射也可不提K而称η为f的核,因此,单态射的核是零态射0,零态射的核是单位态射。
态射的上核态射的上核(cokernel of a morphism)是群论中同态的上核概念的推广(不过,在群论中同态的上核是指一个商群,而在群范畴中是指此商群及群到此商群的满同态),态射的上核是态射的核的对偶概念。设范畴C有零对象(因而有零态射0),f∈Hom(A,B),所谓f的上核coker f,是指C的一个对象W与一个态射π∈Hom(B,W)组成的对(W,π),它满足:1.π是满态射;2.πf=0;3.对任何的g∈Hom(B,C),只要gf=0就必有τ∈Hom(W,C)使τπ=g (条件1可去掉,但在条件3中须强调“必有惟一的τ”)。
在等价意义下,f的上核如存在必惟一.,有时为强调态射也可不提W而称π为f的上核,且记为coker f=π,因此,满态射的上核是零态射0,零态射的上核是单位态射1。
本词条内容贡献者为:
王海侠 - 副教授 - 南京理工大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国