[科普中国]-商范畴

概念

商范畴(quotient category)是代数系的商代数系及局部化的高度推广。若C为一个范畴，二元关系R对C中任两个对象A，B的态射集HomC(A，B)都给出一个二元关系RA，B，则必有一个范畴C/R(其对象类仍为C的对象类)，以及一个函子Q=QR：C→C/R使：

1.若f，f′∈HomC(A，B)且fRA，Bf′，则Qf=Qf′.

2.若D为一个范畴，H：C→D是一个使fRA，Bf′蕴含着Hf=Hf′的函子，则有惟一的函子H′：C/R→D使H′°Q=H.

3.函子Q关于对象是满单的。

由二元关系R必可诱导一个使RR′的最小的二元关系R′，使对任意的A，B，R′AB都是HomC(A，B)上的等价关系.于是按R′A，B可得商集HomC(A，B)/R′A，B.C/R关于A，B的态射集HomC/R(A，B)就取为HomC(A，B)/R′A，B，态射合成按显见的方式定义，这样得出的范畴C/R称为范畴C(关于R)的商范畴.例如取C=Top(对象为拓扑空间，态射为连续映射)，取R为同伦关系，则得C的商范畴C/R，它以拓扑空间A，B，…为对象，而HomC/R(A，B)则为A到B的连续映射之同伦类的集合。对局部小的阿贝尔范畴A，若B为A的塞尔子范畴，则可按下法定义一个范畴A/B，其对象类即A的对象类；其态射集(对任意的对象A，B)定义为：

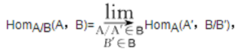
其中，表集范畴中的正向极限，态射合成按显见方式定义。这个范畴A/B就称为A关于B的商范畴。A/B仍为一个阿贝尔范畴。1

范畴范畴是范畴论的基本概念之一。称C是一个范畴，是指C满足下述六点：

1.C有一个对象类{A，B，C，…}(不要求它是一个集合，即不要求它满足集合论的公理，只要求能判别出是不是它的对象)，常记为ObjC或简记C。

2.对C的任两对象A，B，有一个确定的集合(可为空集)Hom(A，B)，其元素称为由A到B的态射，记为f∈Hom(A，B)或f：A→B。

3.对给定的f∈Hom(A，B)与g∈Hom(B，C)有惟一的gf∈Hom(A，C)，称为f与g的合成。

4.Hom(A，B)与Hom(C，D)有公共元是指A=C且B=D。

5.态射合成满足结合律。

6.对C的任意对象A，Hom(A，A)至少有一个元素εA使对σ∈Hom(A，B)恒有σεA=σ=εBσ，称εA为A的恒等态射(εB为B的恒等态射)。

例如，以一切集合作对象，以集合映射作态射，则得集合范畴Set(简称集范畴)。以一切拓扑空间作对象，以连续映射作态射，则得拓扑空间范畴Top。以一切环为对象，以环同态作为态射得环范畴Ring。类似地，可得群范畴Group，阿贝尔群范畴AG，环R上的左R模范畴RM等。以自然数为对象，a|b(表示a整除b)时定义Hom(a，b)有惟一元素φab，ab时定义Hom(a，b)=(空集)，也得到一个范畴.一般地，对每个拟序集都可仿此定义范畴。

商代数商代数是一个代数结构模它的同余关系产生的新的代数结构。

集A上的等价关系～将A划分成互不相交的等价类的并，记成=A/～，即的元素[a]是a所在的等价类。称为A关于～的商集。进一步，设～是代数结构〈A，◦〉上的等价关系，并且对任意a，b∈A，若a～b，对任何c∈A，都有a◦C～b◦c，且c◦a～c◦b，则称等价关系～是〈A，◦〉上的同余关系。例如，模m同余，a≡b (modm)，当且仅当m| (a-b)，是〈Z，+〉上的一个同余关系，并且模m同余也是〈Z，+，·〉上的同余关系。又如，群〈G，·〉的正规子群N确定的陪集关系R，aRb当且仅当ab∈N，是〈G，+〉上的同余关系。

设～是代数结构〈A，◦〉上的同余关系，则可在商集=A/～上定义运算*。

[a1] * [a2]=[a1·a2]

称代数结构〈A/～，*)=〈，* 〉为〈A，◦〉(关于～)的商代数。

例如，剩余类环〈Zm，+，·〉是〈Z，+，·〉的一个商代数，群〈G，·〉关于正规子群N的商群〈G/N·〉就是由N确定的陪集关系确定的商代数。

一个代数结构必定与它的商代数同态，把任一元素对应到这个元素所在的等价类的映射就是代数结构到其商代数的同态映射。反过来，代数结构A的任何一个同态映射可以导出A的一个同余关系～，并得到商代数A/～，A/～必与A的同态象同构。

模范畴模范畴(category of modules)是一种重要的范畴。指所有以模和模之间的同态组成的范畴。利用范畴的观点来讨论模和环是一种重要方法。若A是环，则所有的左A模组成的类和所有左A模M，N之间的模同态HomA(M，N)，以及模的同态的乘法运算法则构成一个范畴，称为左A模范畴，记为：A-Mod。2

同态设E与F为两个群胚，它们的合成法则分别记为⊥与⊤。 称从E到F中的映射f是群胚同态，如果对于E的任一元素偶(x，y)，有：

设E与F为两个幺半群(两个群)，称从E到F中的映射。f是幺半群(群)的同态，如果f是群胚的同态，且E的中性元素的象是F的中性元素。(在群的情况下，后一个条件是自然满足的，但是从加法幺半群N到乘法幺半群N的映射x↦0是群胚的同态， 而并不因此就是幺半群的同态)。

设G为乘法群，而a为G的元素。由关系f(n)=an所定义的从加法群Z到G中的映射f是群的同态。

设A与B为两个环(两个体)，称从A到B中的映射f是环(体)的同态，如果f是加法群的同态，且为乘法么半群的同态。这就是说，对A的任一元素偶(x，y)，有

f(x+y)=f(x)+f(y)f(xy)=f(x)f(y)，

并且f将A的单位元变成B的单位元。

例如，设n为非零自然数；使任一有理整数对应其对模n的剩余类映射是从环Z到环Z/nZ上的同态。设E与F为两个A-代数(两个酉A-代数)。称从E到F中的映射f是A-代数(酉A-代数)的同态，如果它是线性映射，并且是乘法群胚(乘法幺半群)的同态。

例如，设E为交换体K上的非零有限n维向量空间，而B为E的基。则从E的全体自同态之酉代数ℒ(E)到K中元素构成的全体n阶方阵之酉代数Mn (K)中的映射，如果该映射使E的任一自同态对应它在基B中的矩阵，则这一映射是酉代数的同态。3

同态的概念能用抽象的方式加以推广。