[科普中国]-局部代数

概念介绍

局部代数(local algebra)是与局部环相应的一类特殊代数。菲廷(Fitting，H.)证明了：若A模N的自同态代数EndA(N)是局部的，则N不可分解。当A是域F上有限维代数时，其逆亦真。

代数数学的一个分支。传统的代数用有字符 (变量) 的表达式进行算术运算，字符代表未知数或未定数。如果不包括除法 (用整数除除外)，则每一个表达式都是一个含有理系数的多项式。例如： 1/2 xy+1/4z-3x+2/3. 一个代数方程式 (参见EQUATION)是通过使多项式等于零来表示对变量所加的条件。如果只有一个变量，那么满足这一方程式的将是一定数量的实数或复数——它的根。一个代数数是某一方程式的根。代数数的理论——伽罗瓦理论是数学中最令人满意的分支之一。建立这个理论的伽罗瓦(Evariste Galois，1811-32)在21岁时死于决斗中。他证明了不可能有解五次方程的代数公式。用他的方法也证明了用直尺和圆规不能解决某些著名的几何问题(立方加倍，三等分一个角)。多于一个变量的代数方程理论属于代数几何学，抽象代数学处理广义的数学结构，它们与算术运算有类似之处。参见，如： 布尔代数(BOOLEAN ALGEBRA);群 (GRO-UPS);矩阵(MATRICES);四元数(QUA-TERNIONS );向量(VECTORS)。这些结构以公理 (见公理法 AXIOMATICMETHOD) 为特征。特别重要的是结合律和交换律。代数方法使问题的求解简化为符号表达式的操作，已渗入数学的各分支。2

设K为一交换体. 把K上的向量空间E叫做K上的代数，或叫K-代数，如果赋以从E×E到E中的双线性映射.换言之，赋以集合E由如下三个给定的法则所定义的代数结构：

——记为加法的合成法则(x，y)↦x+y;

——记为乘法的第二个合成法则(x，y)↦xy;

——记为乘法的从K×E到E中的映射(α，x)↦αx，这是一个作用法则;

这三个法则满足下列条件：

a) 赋以第一个和第三个法则，E则为K上的一个向量空间;

b) 对E的元素的任意三元组(x，y，z)，有

x(y+z)=xy+xz(y+z)x=yx+zx;

c)对K的任一元素偶(α，β)及对E的任一元素偶(x，y)，有(αx)(βy)=(αβ) (xy).

设A为一非空集合. 赋予从A到K中的全体映射之集ℱ(A，K)以如下三个法则：

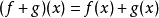
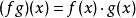
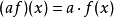则ℱ(A， K)是K上的代数， 自然地被称为从A到K中的映射代数.当A=N时， 代数ℱ(A，K)叫做K的元素序列代数.

无论是在代数还是在分析中，代数结构都是最常见到的结构之一。十九世纪前半叶末，随着哈密顿四元数理论的建立，非交换代数的研究已经开始. 在十九世纪下半叶，随着M.S.李的工作，非结合代数出现了。 到二十世纪初，由于放弃实数体或复数体作为算子域的限制，代数得到了重大扩展。3

与外代数，对称代数，张量代数，克利福德代数等一起，代数结构在多重线性代数中也建立了起来。

局部环局部环和半局部环分别是完全准素环和半准素环概念的推广。环R(≠0)中，若不可逆元(即非单位)集A对于加法是封闭的，则R称为局部环。以下性质是等价的：4

1.R是局部环.

2.R中不可逆元的集A是(双边)理想.

3.A是极大左(右)理想.

4.对于任意r∈R，r或1-r必是左(右)可逆元.

5.R的雅各布森根J(R)是极大左(右)理想.

6.R/J(R)是除环.

7.J(R)=A={x∈R|Rx≠R}(x称为非生成子).

若R/R(J)是半单的，则称R是半局部的。局部环的概念对于模的分解性质十分重要。对于任意R模M，若M的自同态环End(M)是局部的，则M是不可分解的。反之，若M是不可分解且是内射的，则End(M)是局部环。东屋五郎(Azumaya，G.)曾利用局部环的概念，把古典的克鲁尔-锐玛克-施密特定理推广为项数可以是无穷的情形。局部环也具有特殊的同调性质。卡普兰斯基(Kaplansky，I.)于1958年证明：对于局部环R，任意R投射模是R自由的。

人物简介菲廷是德国数学家。在柯尼斯堡工作。主要研究有限群和理想子环论，他引进了所谓菲廷群。长期在哈勒定居，主要研究欧洲中世纪早期的法律史。主张“连续论”，认为中世纪欧洲法学的发展可从注释法学派(即波伦亚学派)的主要代表伊尔内留斯(Imerius)追溯到查士丁尼，找到有关法律学识的直接线索。在所著《中世纪早期有关法律的著作》(1876)和《波伦亚学派的开端》(1888)中发表了这一研究成果。1877年德国民事诉讼法颁布后，主要研究诉讼法，其成果为《德国民事诉讼》(1878)、《德国破产法和破产手续》(1881)。还著有《集团财产的历史发展及其当前的一般作用》(1871)、《伊尔内留斯法典概要》(1894)、《伊尔内留斯法学上的微妙问题》(1894)。5