[科普中国]-BCI商代数

简介

BCI商代数是由日本数学家在K.Isayki年引入的代数结构，它是一类比BCK代数更大的代数类。经过近二十年的发展，这一理论已成为一般代数学中的一个重要分支。自1934年提出代数系统理论以来，代数系统理论引起了很多学者的关注，从而出现了大量超代数的分支，如群、环、BCK代数、格等，代数系统理论在纯粹科学和应用科学的许多方面都有应用。1

背景以集合论和命题演算作为背景，1966年日本数学家Y.Imai和K.Isayki引入了BCK商代数，这样，对一切BCK商代数进行研究和对某些条件下的BCK商代数进行研究，就产生了BCK商代数类和BCK商代数理论一。经过十七八年的发展，这一理论已成为一般代数学中的一个分支这一理论涉及和联系到许多数学分支，如泛代数、群论网、格论冈、布尔代数等作为两类重要的逻辑代数，有很多关于描述一代数理论的文章，但是更多的是关于代数的理想的研究网，模糊理想理论在一代数理论的发展中扮演了很重要的角色。“目前，BCK商代数理论取得了很多丰硕的成果并继续在发展中。2

定义对于任意的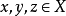 ，如果满足以下条件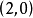， 型代数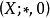 就被称为BCI商代数。

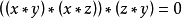
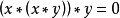
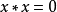
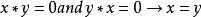
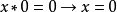
定理（1）任意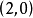 型的代数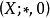 就是BCI商代数，当且仅当它满足：

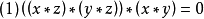
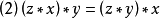
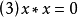
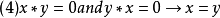
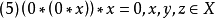
（2）设X是BCI商代数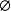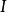，≠包含于X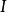，称作X的理想。若

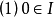
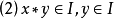
蕴含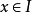成立，这里。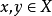

设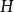≠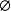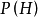，表示H的幂集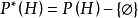，，H上的二元超代数运算“”定义为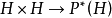，即对于任意的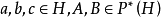，都有下面各式成立：

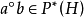
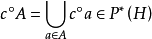
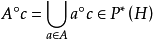
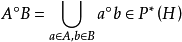
（3）设 f 为BCI商代数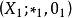到BCI商代数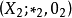的同态映射，则Kerf为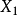的闭理想。3

举例每个阿贝尔群都是BCI商代数， 定义为群减法，0定义为群标识。