[科普中国]-局部表现模

局部表现模(locally presented module)是一种有用的模。若环A是半完全环，则A是序列环的充分必要条件是，每个有限表现左A模是局部表现A模的直和。

概念局部表现模(locally presented module)是一种有用的模。设M是A模，若对任意满同态α：AN→AN″，任意非零同态φ：M→N″和M的任意有限生成子模M′，φ在M′上的限制总可扩张为M′到N的同态，即有同态r：M′→N，使得φ|M′=α°r成立，则称M是局部投射模。对A模M，若有正合序列：Q→P→M→0，其中P和Q都是局部投射模，则称M是局部表现模。当Q，P都是有限生成投射时，M就称为有限表现模。若环A是半完全环，则A是序列环的充分必要条件是，每个有限表现左A模是局部表现A模的直和。1

模一个重要的代数系统。它是一个带算子区A的交换(加)群M。给定集合A与交换群M，若定义了a∈A与x∈M的乘积ax∈M，并且这个积满足条件：

1.a(x+y)=ax+ay (a∈A，x，y∈M)，

则称A为M的算子区，称M为带算子区A的模，又称为A上的模或A模。这时，由对应(a，x)→ax确定的映射A×M→M，称为A作用到M上的运算。任意a∈A可诱导出M的自同态aM：x→ax，而考虑交换群M能否成为A模就是看能否给出映射：μ： A→End(M)， a→aM。

特别地，考虑A是结合环，若满足上述条件1的A模还满足：

2.(a+b)x=ax+bx；

3.(ab)x=a(bx)；

即映射μ：A→End(M)为环同态，则称M为左A模或左环模。由于A到M上的运算是写在左侧，所以M就称为左A模，记为AM。类似地，有右A模M，记为MA。若A有单位元1，且又满足条件

4.1x=x (x∈M)；

则称M为酉模或幺模，以下设A模都是酉模。

同态设E与F为两个群胚，它们的合成法则分别记为⊥与⊤. 称从E到F中的映射f是群胚同态，如果对于E的任一元素偶(x，y)，有：

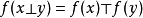设E与F为两个幺半群(两个群)，称从E到F中的映射.f是幺半群(群)的同态，如果f是群胚的同态，且E的中性元素的象是F的中性元素。(在群的情况下，后一个条件是自然满足的，但是从加法幺半群N到乘法幺半群N的映射x↦0是群胚的同态， 而并不因此就是幺半群的同态)。

设G为乘法群，而a为G的元素. 由关系f(n)=an所定义的从加法群Z到G中的映射f是群的同态。

设A与B为两个环(两个体)，称从A到B中的映射f是环(体)的同态，如果f是加法群的同态，且为乘法么半群的同态. 这就是说，对A的任一元素偶(x，y)，有f(x+y)=f(x)+f(y)f(xy)=f(x)f(y)，并且f将A的单位元变成B的单位元。

例如，设n为非零自然数；使任一有理整数对应其对模n的剩余类映射是从环Z到环Z/nZ上的同态。设E与F为两个A-代数(两个酉A-代数)。称从E到F中的映射f是A-代数(酉A-代数)的同态，如果它是线性映射，并且是乘法群胚(乘法幺半群)的同态。

例如，设E为交换体K上的非零有限n维向量空间，而B为E的基. 则从E的全体自同态之酉代数ℒ(E)到K中元素构成的全体n阶方阵之酉代数Mn (K)中的映射，如果该映射使E的任一自同态对应它在基B中的矩阵，则这一映射是酉代数的同态。2

序列环一类特殊环。指可表为其单侧理想有线性序的(单侧)理想的有限直和的环类。一个模M，若它的子模对包含关系(AB或BA)是线性序，则称M是单列模。环R当看做左正则模RR是有限个单列模的直和时，称R是左序列环.同样地，可定义右序列环，但R是左序列环未必为右序列环。若环R是左序列环也是右序列环，则称R是序列环.任何阿廷主理想环皆为序列环。若R是左遗传环且任意左R模的内射包是平坦的，则R的任意左阿廷商环是左序列环。克德(Ko¨the，G.)于1935年首先引入了阿廷序列环并称之为单列环。中山正(Nakayama，T.)于1940年称之为广义单列环。在有些文献中，单列环一词通常用来指准素可分解的阿廷序列环。浅野启三(Asano，K.)于1949年曾刻画阿廷序列环为任意单侧理想都是主理想的环。阿廷序列环是特殊的QF环，它也具有良好的同调性质。毕尔德(Byrd，K.A.)于1970年证明：环R是序列环当且仅当任意R模是拟内射的；又当且仅当它是拟投射的。

本词条内容贡献者为:

王海侠 - 副教授 - 南京理工大学