[科普中国]-微分理想

概念

微分理想(differential ideal)是平行于通常环的理想。设R是有微分系Δ的微分环，R的理想I称为R的微分理想，或Δ理想，是指I也是有微分系Δ的微分环。R至少有两个微分理想{0}和R，称为R的平凡微分理想。其余的微分理想称为非平凡微分理想或真微分理想。有微分系Δ的环R的理想I是Δ理想的充分必要条件是：a∈I，δ∈Δ，有δa∈I或δII。当Δ={δ}时，Δ理想又记为δ理想。对于任意给定的R的一个理想J，若：1

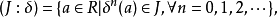
则(J∶δ)是包含在J中最大的R的δ理想。

环环是对并与差运算封闭的集类，测度论中重要概念之一。设F是Ω上的一个非空集类。如果它对集的并及差运算封闭，即对任何A，B∈F，都有A∪B∈F，A\B∈F，则称F为Ω上的环。例如，若F是由实直线R上任意有限个左开右闭的有限区间的并集：

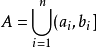
的全体构成的集类，则F是R上的一个环.环也是对于交与对称差运算封闭的集类，并按这两种运算成为布尔环。要把R上的勒贝格测度和勒贝格-斯蒂尔杰斯测度以及相应的积分理论推广到更一般的集合上，就需要做一系列奠基工作，其中之一是建立一些特殊的集类并研究其性质.环以及半环、σ环、代数、σ代数等重要集类正是为了这一目的而引入的。

环论环论是抽象代数学的主要分支之一。它是具有两个运算的代数系.在非空集合R中定义加法“+”和乘法“·”运算，使得R中任意元a，b，c适合条件：

1.R对加法为交换群，称为R的加法群，记为(R，+);

2.R对乘法适合结合律，即(R，·)是半群，称为R的乘法半群;

3.乘法对加法的左、右分配律成立，即

a·(b+c)=a·b+a·c (左分配律)，

(b+c)·a=b·a+c·a (右分配律);

则称R为结合环，简称环(通常a·b写为ab)。它是环论研究的主要对象。环论起源于19世纪关于实数域的扩张与分类，以及戴德金(Dedekind，J.W.R.)、哈密顿(Hamilton，W.R.)等人对超复数系的建立和研究。韦德伯恩(Wedderburn，J.H.M.)于1907年给出的结构定理给出代数研究的模式，也成为环结构研究的模式。20世纪20-30年代，诺特(Noether，E.)建立了环的理想理论，阿廷(Artin，E.)又将代数结构定理推广到有极小条件的环。同时，对非极小条件的环，冯·诺伊曼(von Nenmann，H.)建立了正则环理论，相继盖尔范德(Гельфанд，И.М.)创立了赋值环，克鲁尔(Krull，W.)建立了局部环理论，以及哥尔迪(Goldie，A.W.)完善了极大条件环理论。

20世纪40年代，根论迅速发展，尤其是雅各布森(Jacobson，N.)于1945年引入的被称为雅各布森根的概念后，建立了本原环理论、半本原环的结构定理与本原环的稠密性定理，完善和深化了不带附加条件环的理论.20世纪50年代中期，阿密苏(Amitsur，S.A.)、库洛什(Kurosh，A.)创立了根的一般理论，环论已趋完善。

另一方面，由群表示研究的影响，产生模、群环与分次环的理论.20世纪20年代初，诺特引入了模的概念，并研究模对有限群表示的作用与环结构之间的关系，用模的语言去刻画环，特别是20世纪50年代以后，同调代数的迅速发展，使环的理论进入更高层次虽然，早在1854年，凯莱(Cayley，A.)就引入了群代数，然而，它的研究是从20世纪30年代开始直到60—70年代，受群表示论与环的理论的推动才蓬勃发展起来的.20世纪70年代后，由于分次代数的推动，群代数进入新的阶段——交叉积的研究.分次环与模发展的另一动力是交换代数几何中射影代数簇，20世纪70年代以来，由于非交换代数几何及群表示论的推动，环论已进入一个新的阶段。2

理想理想是集合论中的基本概念之一。设S为任意集合，若I⊆P(S)且满足：

1.∅∈I;

2.若X，Y∈I，则X∪Y∈I;

3.若X，Y⊆S，X∈I，Y⊆X，则Y∈I;

则称I为集合S上的理想。理想的概念在现代数学的几乎每个分支中均有应用，且有许多变体或引申。例如，布尔代数上的理想即为集合上的理想的一种变体。设B为任意布尔代数，若B的一个子集I满足：

1.0∈I，1∉I(其中0，1分别为布尔代数B中的零元与么元);

2.对任何u∈I，v∈I，有u+v∈I;

3.对任何u，v∈B，若u∈I且v≤u，又v∈I;

则称I为B上的理想。

微分环微分环是带导子集的环。若环R有一个导子集合Δ，则Δ称为R的微分系，R称为有微分系Δ的环，或简称微分环或Δ环。设S是有微分系Δ的环R的子环，若S也是有微分系Δ的环，则S称为R的微分子环，或Δ子环，而R称为S的微分扩环。R至少有两个Δ子环{0}和R，称为R的平凡微分子环。其余的微分子环称为非平凡微分子环，或真微分子环。有微分系Δ的环R的子环S是Δ子环的充分必要条件是：a∈S，δ∈Δ，有δa∈S.Δ={δ}时，Δ环及Δ子环分别记为δ环，δ子环。3