定义
设f(n)、g(n)是两个数论函数,它们的Dirichlet(狄利克雷)乘积也是一个数论函数,其定义为:1

简记为h(n)=f(n)*g(n)。
函数f(n)与g(n)的狄利克雷乘积也可以表示为

性质狄利克雷乘积有以下基本性质:2
1.满足结合律。设f,g,h为任意三个数论函数,则(f*g)*h=f*(g*h)。
2.满足交换律。设f,g为任意二个数论函数,则f*g=g*f。
3.对于所有的数论函数f(n),均有f(n)*I(n)=I(n)*f(n)=f(n),故I(n)在狄利克雷乘积中有单位元的作用,简称I(n)为单位数论函数,或称I(n)为卷积单位元。
4.若f(n),g(n)均为积性函数,则f*g亦为积性函数,反之,若g(n)与(f*g)(n)都是积性函数,则f(n)亦为积性函 数。特别地,当F=f*μ为积性函数时,f(n)亦为积性函数。
5.若g(n)是完全积性函数,且h=f*g,则f=h*μg,即若
 则
则

常用乘积常用的狄利克雷乘积有2:
1.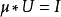 ,即
,即
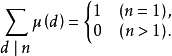 2.
2.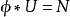 ,其中N(n)=n,即
,其中N(n)=n,即
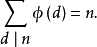
3. ,其中N(n)=n,即
,其中N(n)=n,即

4.
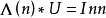
5.
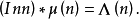




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国