[科普中国]-包含关系

简介定义

包含是集合与集合之间的从属关系，也叫子集关系。基本含义近同于蕴含、蕴涵、包涵，关系形容词。出自汉·桓宽《盐铁论·地广》：“王者包含并覆，普爱无私，不为近重施，不为远遗恩。”。

分类（1）包含于（包含）1

（2）真包含（真包含于）2

性质（1）传递性：若集合A包含于集合B，集合B包含于集合C，那么集合A包含于集合C。

（2）归属性：集合A包含于集合B，那么集合A在集合B里面，归属于B。

概率名词简介实际中，在一个随机现象中常会遇到许多事件，它们之间有下列三种关系。

(1)包含：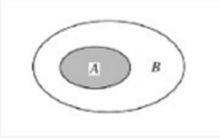

在一个随机现象中有两个事件A与B。若事件A中任一个样本点必在B中，则称A被包含在B中，或B包含A，记为“A包含于B”：A⊂B或“B包含A”：B⊃A，这时事件A的发生必导致事件B发生。如右图所示。如掷一颗骰子，事件A=“出现4点”必导致事件B=“出现偶数点”的发生，故A⊂B。

(2)互不相容：

在一个随机现象中有两个事件A与B。若事件A与B没有相同的样本点，则称事件A与B互不相容。这时事件A与B不可能同时发生。如图所示，如在电视机寿命试验里“电视机寿命小于1万小时”与“电视机寿命超过4万小时”是两个互不相容事件，因为它们无相同的样本点?或者说它们不可能同时发生。

两个事件间的互不相容性可推广到三个或更多个事件间的互不相容。例如在检查三个产品时候，C1=“恰有一件不合格品”，C2=“恰有两件不合格品”，C3=“全是不合格品”，C0=“没有不合格品”是四个互不相容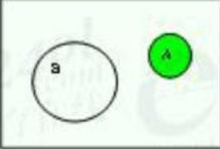事件。

(3)相等:

在一个随机现象中有两个事件A与B。若事件A与B含有相同的样本点，则称事件A与B相等，记为A=B。如在掷两颗骰子的随机现象中，其样本点记为(x，y)，其中x与y分别为第一与第二颗骰子出现的点数，如下两个事件:A={(x，y):x+y=奇数}，B={(x，Y):x与y的奇偶性不同}，可以验证A与B含有相同的样本点，故A=B。

举例元素和集合之间的互相包含的关系叫“属于”，而不能说成包含，包含只能用于集合与集合之间。
例A={1,2},B={1,2,3}
则1∈A,2∈A,3∈B
属于是元素和集合之间的关系，例如，元素a属于集合A，记为a∈A
属于符号：∈,用于元素与集合之间

集合与集合之间的包含才叫包含
如果集合A的任意一个元素都是集合B的元素，那么集合A叫做集合B的子集，记作A包含于B或B包含A
空集被任一一个集合所包含，就是任何集合的子集
如果集合A的元素是集合B的子集，并且B中至少有一个元素不属于A，那么集合A叫做集合B的真子集，记作A真包含于B或B真包含A。