正规闭包(normal closure)是一种特殊的正规子群,群中包含某个子集的最小正规子群。代数扩张K/F称为正规扩张,是指F[X]中每个在K中有根的既约多项式,在K[X]中可以分解为一次因子的乘积,它等价于K的任意元α在F上的最小多项式在K[x]中可以分解为一次因子的乘积。一个代数扩张K/F的正规闭包是指F的一个正规扩张,它包含K且它包含的K的任意真子域在F上都不是正规的。
基本介绍正规扩张(normal extension)是一种重要的代数扩张,它与多项式的分裂域密切相关,代数扩张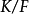 称为正规扩张,是指
称为正规扩张,是指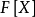 中每个在
中每个在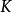 中有根的既约多项式,在
中有根的既约多项式,在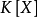 中可以分解为一次因子的乘积,它等价于
中可以分解为一次因子的乘积,它等价于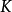 的任意元
的任意元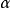 在
在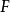 上的最小多项式在
上的最小多项式在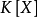 中可以分解为一次因子的乘积。一个代数扩张
中可以分解为一次因子的乘积。一个代数扩张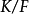 的正规闭包是指
的正规闭包是指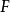 的一个正规扩张,它包含
的一个正规扩张,它包含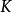 且它包含的
且它包含的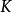 的任意真子域在
的任意真子域在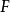 上都不是正规的。值得注意的是,即使
上都不是正规的。值得注意的是,即使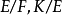 是正规扩张,也不能推出
是正规扩张,也不能推出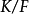 是正规的。例如,对域链
是正规的。例如,对域链
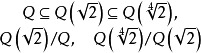 都是正规的,但
都是正规的,但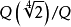 不是正规的1。
不是正规的1。
相关定义及定理定义1 设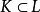 为域扩张,
为域扩张,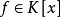 ,如果
,如果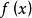 在
在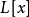 中完全分解为一次因子的积,则称
中完全分解为一次因子的积,则称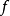 在
在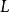 中分裂。
中分裂。
定义2 一个域扩张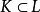 称作正规的,如果
称作正规的,如果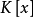 中的任一不可约多项式若在
中的任一不可约多项式若在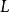 中有零点则在
中有零点则在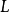 中分裂2。
中分裂2。
命题1 对一个有限域扩张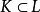 ,下列三条件等价:
,下列三条件等价:
i) L是K的正规扩域;
ii) L是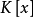 中一个多项式的分裂域;
中一个多项式的分裂域;
iii) 对任一域扩张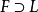 及任意
及任意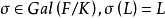 。
。
注1 对无限代数扩张,只要将ii)中的“一个多项式”改为“一组多项式”,命题1仍成立(在多项式个数不可数的情形需要用超限归纳法证明)。
定义3 设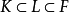 为域扩张,其中F是K的正规扩域,如果F的任一包含L的真子域都不是K的正规扩域,则称F为L在K上的一个正规闭包(直观地说它是K的包含L的最小正规扩张)。
为域扩张,其中F是K的正规扩域,如果F的任一包含L的真子域都不是K的正规扩域,则称F为L在K上的一个正规闭包(直观地说它是K的包含L的最小正规扩张)。
推论1 对任意代数扩张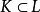 存在正规闭包F,它是L中所有元在K上的定义多项式的一个分裂域,且
存在正规闭包F,它是L中所有元在K上的定义多项式的一个分裂域,且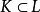 的正规闭包在
的正规闭包在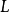 -代数同构之下是唯一的。此外,任意
-代数同构之下是唯一的。此外,任意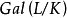 的元可以扩张为
的元可以扩张为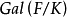 的元。
的元。
推论2 设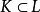 为域扩张,如果存在一个K的正规扩域
为域扩张,如果存在一个K的正规扩域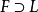 使得对任意
使得对任意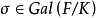 有
有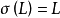 ,则
,则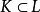 为正规扩张2。
为正规扩张2。
本词条内容贡献者为:
尚华娟 - 副教授 - 上海财经大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国