[科普中国]-经典伴随变换

经典伴随变换(classical adjoint transformation)是向量空间中的一种线性变换。在线性代数中，一个方形矩阵的伴随矩阵是一个类似于逆矩阵的概念。如果矩阵可逆，那么它的逆矩阵和它的伴随矩阵之间只差一个系数。然而，伴随矩阵对不可逆的矩阵也有定义，并且不需要用到除法。

定义参见：子式和余子式、余因子矩阵和转置矩阵

设R是一个交换环，A是一个以R中元素为系数的n×n的矩阵。A的伴随矩阵可按如下步骤定义：

定义：A关于第i行第j列的余子式（记作Mij）是去掉A的第i行第j列之后得到的(n− 1)×(n− 1)矩阵的行列式。

定义：A关于第i行第j列的代数余子式是：

定义：A的余子矩阵是一个n×n的矩阵C，使得其第i行第j列的元素是A关于第i行第j列的代数余子式。

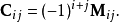引入以上的概念后，可以定义：矩阵A的伴随矩阵是A的余子矩阵的转置矩阵：

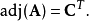
也就是说，A的伴随矩阵是一个n×n的矩阵（记作adj(A)），使得其第i行第j列的元素是A关于第j行第i列的代数余子式：

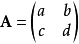例子2x2矩阵一个 矩阵 的伴随矩阵是

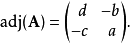
3x3矩阵对于 的矩阵，情况稍微复杂一点：

其伴随矩阵是：

其中

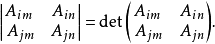
要注意伴随矩阵是余子矩阵的转置，第3行第2列的系数应该是A关于第2行第3列的代数余子式。

具体情况对于数值矩阵，例如求矩阵

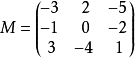
的伴随矩阵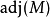 ，只需将数值代入上节得到的表达式中。例如第2行第3列的代数余子式为

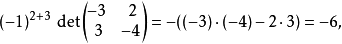
因此伴随矩阵中第3行第2列的位置上是-6。

计算后的结果是：

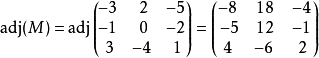
应用作为拉普拉斯公式的推论，关于n×n矩阵A的行列式，有：

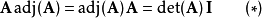
其中I是n阶的单位矩阵。事实上，Aadj(A)的第i行第i列的系数是

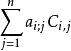。根据拉普拉斯公式，等于A的行列式。

如果i≠j，那么Aadj(A)的第i行第j列的系数是

。拉普拉斯公式说明这个和等于0（实际上相当于把A的第j行元素换成第i行元素后求行列式。由于有两行相同，行列式为0）。

由这个公式可以推出一个重要结论：交换环R上的矩阵A可逆当且仅当其行列式在环R中可逆。

这是因为如果A可逆，那么

，

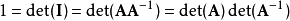如果det(A)是环中的可逆元那么公式（*）表明

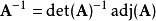
性质对n×n的矩阵A和B，有：

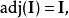
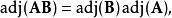
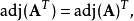
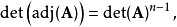
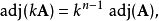
当n>2时，

如果A可逆，那么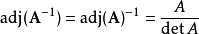

如果A是对称矩阵，那么其伴随矩阵也是对称矩阵；如果A是反对称矩阵，那么当n为偶数时，A的伴随矩阵也是反对称矩阵，n为奇数时则是对称矩阵。

如果A是（半）正定矩阵，那么其伴随矩阵也是（半）正定矩阵。

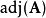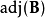如果矩阵A和B相似，那么和也相似。

如果n>2，那么非零矩阵A是正交矩阵当且仅当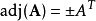

伴随矩阵的秩当矩阵A可逆时，它的伴随矩阵也可逆，因此两者的秩一样，都是n。当矩阵A不可逆时，A的伴随矩阵的秩通常并不与A相同。当A的秩为n-1时，其伴随矩阵的秩为1，当A的秩小于n-1时，其伴随矩阵为零矩阵。

伴随矩阵的特征值设矩阵A在复域中的特征值为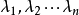(即为特征多项式的n个根），则A的伴随矩阵的特征值为。

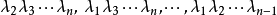伴随矩阵和特征多项式设p(t) = det(A−tI) 为A的特征多项式，定义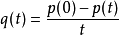，那么：

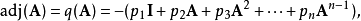
其中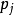是p(t)的各项系数：

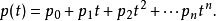
伴随矩阵也在行列式的导数形式中3。

本词条内容贡献者为:

王海侠 - 副教授 - 南京理工大学