[科普中国]-完全对称化子

概念

完全对称化子是张量空间上的一种投影算子。有时也称为对称化子。设E是特征为0的域K上的向量空间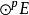，为E的p次张量幂，p≥2，若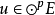，Sp是p阶对称群，对任意σ∈Sp，σu=u，则u称为对称张量。若：

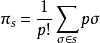则πs是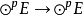的线性映射，称为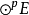上的对称化子。πsu称为u的对称部分。若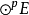中对称张量所成的子空间为Yp(E)，Mp(E)为{u-τu|u∈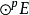，τ∈sp}生成的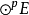之子空间，则：1

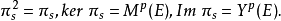并且，

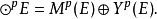
向量空间设K为交换体。称赋以由下列两个给定法则所定义的代数结构的集合E为K上的向量空间：

——记为加法的合成法则，

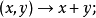——记为乘法的作用法则，即从K×E到E中的映射，

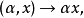
这两个法则满足下列条件：

a)赋以加法的集合E是交换群；

b) 对K的任一元素偶(α，β)，以及对E的任一元素x，α(βx)=(αβ)x；

c) 对E的任一向量x，1x=x，其中1表示体K的单位元素；

d)对K的任一元素偶(α，β)，以及对E的任一元素偶(x，y)，(α+β)x=αx+βx，α(x+y)=αx+αy。

当体K不再假定为交换的时，满足上述条件的集合E称为K上的左向量空间。

如果条件α(βx)=(αβ)x换为α(βx)=(βα)x，则称E为K上的右向量空间。在这种情况下，E上的作用法则记为：

例如，设K为交换体，而E为只有一个记为0的元素的集合。E赋以两个法则：(0，0)↦0，(α， 0)↦0则E为K上的向量空间。

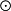张量空间多重线性代数的重要概念。定义有张映射的一种向量空间。具体定义有多种不同的形式。例如，可定义为：设P是一个向量空间，若存在张映射：V1×V2×…×Vm→P使得〈Im〉=P，则称P为V1，V2，…，Vm的带有张映射的张量空间；或称P为V1，V2，…，Vm的张量积空间；或简称P为V1，V2，…，Vm的张量积，记为：2

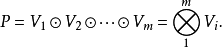张量空间对于多重线性代数的重要性如同向量空间对于线性代数的重要性。张量空间的维数是：

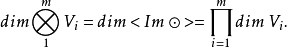
投影算子把任一元映到该元的正交投影的算子。设M是希尔伯特空间H的闭线性子空间.对任意x∈H，必有分解x=x1+x2，x1∈M，x2∈M，定义算子P如下：Px=x1，即Px是x在M上的投影，称算子P为由H到M上的正交(或直交)投影算子，简称投影(或射影)算子。投影算子P具有下列性质：P=P(幂等)；P有界(事实上有‖P‖=1)；对一切x，y∈H，(Px，y)=(x，Py)成立(自伴)。反之，H上有界自伴的幂等算子必是投影算子.正交投影算子与H的闭线性子空间之间成一一对应。满足PQ=0的两个正交投影算子P和Q称为相互正交的，记为P⊥Q。

正交投影算子是希尔伯特空间上特别重要的一类算子。它是希尔伯特空间的很好的几何特征的反映，又是研究其他复杂算子的工具。

张量n维空间中的一个量，它具有nr个分量，用Ti1，i2，…，ir表示，它的每个分量都是坐标的函数；在坐标变换下，这些分量按照一定的规律作线性变换。r称为张量的阶。

张量是矢量及矩阵概念的推广。标量是零阶张量；向量是一阶张量；矩阵是二阶张量。三阶张量(它的分量用Tijr表示)就像是一个“立体矩阵”。

在1900年，张量首先在弹性理论中使用。“张量”原来的含义是“张紧”与“张开”。

1892年起，里奇(C.G.Ricci，意，1853—1925)与列维·奇维塔(T.Levi-Civita，意，1873—1941)开始建立张量分析的理论，成为黎曼几何与广义相对论的一种工具。

为了简便，在张量列式或计算时，常按求和约定将求和号略去。3

对称张量各分量关于指标对称的张量，即在正整数{1，2，…，r}的置换作用下不变的r阶反变张量。记Tr(V)=Vr，o，它表示r阶反变张量全体。P(r)表示{1，2，…，r}的置换群。设x∈T(V)，若对任意的σ∈P(r)，都有σx=x，则称x是对称的r阶反变张量。若对任意的σ∈P(r)，都有σx=sgn σ·x，其中sgn σ表示置换σ的符号，即：

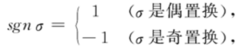
则称x是反对称r阶反变张量。设x∈T(V)，则x是对称张量的充分必要条件是它的分量关于各指标是对称的。x是反对称张量的充分必要条件是它的分量关于各指标是反对称的。