[科普中国]-局部群系

局部群系(local formation of groups)是借助于主因子由一组群系来定义的群系。群系是对取同态像与取有限次直积封闭的群类。

概念局部群系(local formation of groups)是借助于主因子由一组群系来定义的群系。若对每个素数p给定了一个群系F(p)，则可按下述方式规定一个有限群的群系F：有限群G∈F，当且仅当对G的每个主因子H/K及|H/K|的每个素因数p，

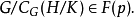这里CG(H/K)是G的所有这样的元构成的子群，它们在H/K上的共轭作用是平凡作用，所以G/CG(H/K)就是G在H/K上共轭作用产生的自同构群。这样决定的群系F称为由{F(p)}局部定义的群系，简称F为局部系；{F(p)}称为F的定义系。从群对它的各个主因子的作用情况来研究群，是有限可解群论的常用研究手法之一，这是局部群系概念的来源。而这个概念也正好高度概括了这种研究思想。

群系对取同态像与取有限次直积封闭的群类。若群类F满足以下两个封闭条件，则称此群类为群系：

1.若群G在F中，则G的任何同态像也在F中。1

2.若MG，NG，G/M∈F，G/N∈F，则G/M∩N∈F。

自1963年格舒兹(Gaschütz，W.)引入群系概念并作出一些令人感兴趣的结果以后，群系理论发展很快，各种群类的概念也应运而生。群系理论最初的成功在于它概括并发展了有限可解群的一些重要理论，提炼出了许多好概念。群系理论现已不仅仅限于有限可解群，也不仅仅用来研究群的群论性质与构造，群系本身的性质与构造也成为吸引人的课题.群的性质与群系作为一个整体的性质，二者交互作用，相互影响，使群系理论充满活力。

有限群具有有限多个元素的群，是群论的重要内容之一。其所含元素的个数，称为有限群的阶。历史上，抽象群论的许多概念起源于有限群论。有限群可分为两大类：可解群与非可解群(即单群)。

有限群的研究起源很早，其形成时期是与柯西、拉格朗日、高斯、阿贝尔以及后来的伽罗瓦、若尔当等人的名字相联系的。如何确定可解群和单群是抽象群理论建立后的一个重要发展方向。德国数学家赫尔德在1889年以后的若干年内，详细地研究了单群和可解群，证明：一个素数阶循环群是单群，n个(n≥5)文字的全部偶置换组成的交换群是单群。他还发现了许多其他有限的单群。赫尔德和若尔当还建立了在有限群中的若尔当—赫尔德合成群列和若尔当—赫尔德定理。在19世纪末，德国数学家弗罗贝尼乌斯、迪克和英国数学家伯恩塞德等都致力于可解群的研究。20世纪初伯恩塞德证明的关于pq(p、q是素数)必是可解群的定理，导致了对有限单群进行分类的重要研究。美国数学家汤普森和菲特在20世纪60年代初证明了有限群中长期悬而未决的一个猜想(见伯恩塞德猜想)：奇数阶群一定是可解群。它推动了有限群理论的发展。有限单群的完全分类，即找出有限单群所有的同构类，经过上百名数学家约40年的共同努力，终于在1981年得到解决，这是数学史上的一个非凡成就。

群论群是现代数学中最重要的具有概括性的概念之一，有关群的性质及其结构的理论称为群论。

1831年，年仅20岁的青年数学家伽罗华得到n次方根可否通过对系数施行四则 和开方运算来求解的判据，一举解决了五 次以上代数方程求解的千古难题。这个问 题得以解决，取决于他对置换群性质所作 的深入讨论，群的概念就在这时产生了。 现在研究代数方程的性质与群的性质之间 的关系已成为一门大理论伽罗华理论所研 究的对象，伽罗华理论在群论的发展中起 作决定性的作用。40年后克莱因的变换群 导致几何观的一次革命; 索福斯·李研究 微分方程，开创李群论，更深刻影响着数 学物理的发展。在数学物理的对称现象的 研究中，对称的概念看来是明显的，但对 对称概念的精确和一般的描述，特别是对 称性质量上的计算，却要用群论这个工具 才行。19世纪到20世纪，在几何、晶体等 物理、化学中，都弄清了对称规律的重要 意义，因此群论的方法和结果得以广泛使 用。1890年，费道洛夫用群论阐明晶体结 构的几何形态，特别是20世纪30年代， 书尔、维格纳等人把群论应用于量子力学 取得成功，导致了原子、分子结构的重要 发现。现在群论已经是量子物理和量子化 学常用的工具了，这更使群论走出了纯数 学专业的数学王国，活跃于更广阔的科学 地。今天，群的概念已普遍被认为是数学 及其许多应用中最基本的概念之一，它不 但渗透到像几何学、代数拓扑学、函数论、 泛函分析及其他许多数学分支中而着重要 的作用，还形成了一些新学科，如拓扑群、 李群、代数群、算术群等。它们还具有与 群结构相联系的其他结构，如拓扑、解析 流形、代数簇等，并在结晶学、理论物理、 量子化学以至编码学、自动机理论等方面 都有重要应用。作为推广 “群” 的概念的 产物，群论及其在计算机科学中的应用， 也有很大的发展。

群的概念中有两个方面： 一是指出它的元素是哪些事物，二是元素间运算的规则，可分别用它们来研究群。研究群的元素和元素集合的各种性质，以及它们同群的运算性质之间的联系，这常常是研究各 种具体的群，如交换群、置换群、运动群、 拓扑群等；也可研究完全由群的运算性质表示出来的特性，它属于抽象群论或一般 群论。下面是一些抽象群论的概念： 同构， 一个群的元素与另一个群的元素对应，运 算结果也是对应的，称两个群同构； 一个群所含元素的个数称为群的阶，群G的阶 记为|G| ，|G|有限时为有限群，无限 时为无限群；同构中两个群中的元素是一一对应的，若存在多对一的对应则称为同态。2

本词条内容贡献者为:

王海侠 - 副教授 - 南京理工大学