简介
交错多重线性映射(alternating multilinear mapping)是一种特殊的反对称多重线性映射。设
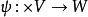 为多重线性映射(其中V,W都是域K上的线性空间),若对任意的
为多重线性映射(其中V,W都是域K上的线性空间),若对任意的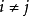 ,当
,当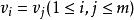 时,必有
时,必有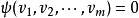 ,则称
,则称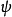 为交错多重线性映射。由于偶(奇)置换必可分解为偶(奇)数个对换之积,利用
为交错多重线性映射。由于偶(奇)置换必可分解为偶(奇)数个对换之积,利用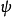 的多重线性性质展开
的多重线性性质展开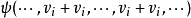 ,即知交错多重线性映射一定是反对称多重线性映射,反过来未必成立,但在K的特征不为2(特别是K的特征为0,例如K=C时)二者是等价的概念。2
,即知交错多重线性映射一定是反对称多重线性映射,反过来未必成立,但在K的特征不为2(特别是K的特征为0,例如K=C时)二者是等价的概念。2
性质E及F重新表示两个赋范巴拿赫空间。
命题:设f∈£p(E;F)是一个交错多重线性映射,那么:
(1)每当对于一对不同的指标(i,j),我们有xi=xj时,就有f(x1,…,xp)=0;
(2)对于序列[1,…,p]的任何排列σ,我们有
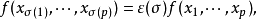 其中ε(σ)=±1是排列σ的标记。1
其中ε(σ)=±1是排列σ的标记。1
反对称多重线性映射一类重要的多重线性映射。关于G和χ对称的多重线性映射
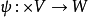 当G=Sm,χ=ε(称号特征标,σ∈Sm为偶(奇)置换时ε(σ)=1(-1))时,称为反对称多重线性映射,简称反对称映射。或等价地定义为:当对任意σ∈Sm有
当G=Sm,χ=ε(称号特征标,σ∈Sm为偶(奇)置换时ε(σ)=1(-1))时,称为反对称多重线性映射,简称反对称映射。或等价地定义为:当对任意σ∈Sm有
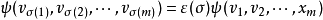 时,称
时,称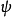 为反对称多重线性映射。当域K的特征为0时,多重线性映射
为反对称多重线性映射。当域K的特征为0时,多重线性映射
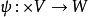 为反对称的当且仅当对任意的(i≠j),当
为反对称的当且仅当对任意的(i≠j),当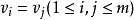 时,有
时,有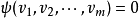 。在域K之特征非0时,这二者未必等价。2
。在域K之特征非0时,这二者未必等价。2
交错多重线性映射的乘法设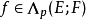 并且
并且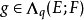 为了定义 f 及 g 之间的乘积,必须先给出一个连续双线性映射
为了定义 f 及 g 之间的乘积,必须先给出一个连续双线性映射
 (在一个赋范e.v.H中取值)。于是连带着 f 及 g,可取一映射
(在一个赋范e.v.H中取值)。于是连带着 f 及 g,可取一映射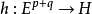 ,即
,即
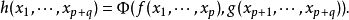 映射 h 显然是连续多重线性的。但它一般不是交错的:它只属于(p+q)重线性映射的向量空间;这种映射作为前p个变量
映射 h 显然是连续多重线性的。但它一般不是交错的:它只属于(p+q)重线性映射的向量空间;这种映射作为前p个变量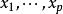 的映射是交错的,作为后q个变量
的映射是交错的,作为后q个变量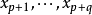 的映射也是交错的,把这种空间记作
的映射也是交错的,把这种空间记作 。1
。1




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国