[科普中国]-极小化问题

极小化问题是求出与给定电路等效的一个（或所有）最简电路的问题。实际上极小化问题就是求与给定真值函数（一种特殊的布尔函数）的一个（或所有）最简的等值函数。

定义极小化问题是求出与给定电路等效的一个（或所有）最简电路的问题。实际上极小化问题就是求与给定真值函数（一种特殊的布尔函数）的一个（或所有）最简的等值函数。较复杂的开关函数，常可化成与它相等但形式较简单的开关函数。

例如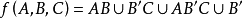， 与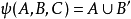相等，但 ψ 比 f 简单，实现 ψ 的组件比实现 f 的组件要少许多，而它们的逻辑功能却相同。因此，用电路 ψ 来取代 f 既符合节省原则，而且还可提高效率，所以极小化问题是开关电路中的重要研究课题。求最简电路的方法有多种，如代数化简法，奎因一麦克勒斯基法，嘎柴拉法及卡诺图法等。1

真值函数真值函数亦称真值函项。一种特殊函数。指以真值集 {T,F} 为定义域和值域的函数。根据真值函数的变元个数，真值函数可为一元真值函数，二元真值函数······ n 元真值函数等。对任意的自然数 n≥1，总有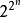个不同的 n 元真值函数。

开关函数一个具有两种状态的电子元件称为一个开关。它可由普通的一个开关或联动开关组成。每一个开关的状态由一个开关变量来表示，例如用A表示一个开关变量，用0, 1表示一个开关的两个状态，则开关变量A的取值是0或1。开关函数就是用来表示电子元件状态的函数。

本词条内容贡献者为:

王海侠 - 副教授 - 南京理工大学