定义
设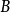 是一个布尔代数,所谓
是一个布尔代数,所谓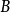 上的n元布尔方程是指如下的含有n个待定元的布尔函数f(X)及g(X)所组成的等式
上的n元布尔方程是指如下的含有n个待定元的布尔函数f(X)及g(X)所组成的等式
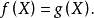
类似的,我们可用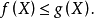
及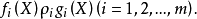
分别定义布尔不等方程及(广义)布尔方程组,其中“ ”既可以是“=”,也可以是“≤”,布尔方程的(特)解是指满足
”既可以是“=”,也可以是“≤”,布尔方程的(特)解是指满足 的一个向量X∈
的一个向量X∈ ;布尔不等方程及(广义)布尔方程组的(特)解的定义类似2。
;布尔不等方程及(广义)布尔方程组的(特)解的定义类似2。
0-1布尔方程定义 若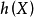 是布尔函数,
是布尔函数, ,则
,则
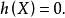
及
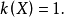
分别称为(布尔)0方程与(布尔)1方程,它们又合称为**(布尔)0-1方程或0-1****布尔方程**。2
1元布尔方程仅含1个特定元的(广义)布尔方程,简称为1元(广义)布尔方程2
由下文定理1知,每一个1元广义布尔方程都可以写成如下的0方程
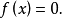
这个0方程必定可写成如下的标准形
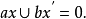
其中a,b为布尔常量。
在每一个方程中都要区分哪些是待定元(未知元),哪些是系数(已经给定的元),例如,在1元标准形布尔方程
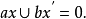
中,x(及x’)是未知元,而a与b是系数,但是在通常的定理中则没有此种区别。
重要定理定理1每一个形如2
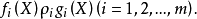
的广义布尔方程(m=1的情况)或广义布尔方程组(m>1的情况)都等价于一个0-1布尔方程。
定理2若B是布尔集;a,b∈B,则下列语句等价:2
①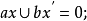
②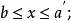
③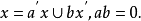
④1元布尔方程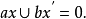 是否有解(即:是否存在一个x∈B)使上式成立与系数a与b有关,方程
是否有解(即:是否存在一个x∈B)使上式成立与系数a与b有关,方程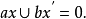 有解的充要条件是有:
有解的充要条件是有:
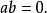
此外,x是1元布尔方程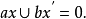 的解的充要条件是
的解的充要条件是
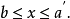
定理3若ab=0,则2
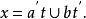 及
及
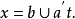




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国