[科普中国]-样本分布函数

定义样本分布函数

我们知道，若总体是随机变量X，则X的分布就是总体的分布(也叫理论分布)，X的分布函数便是总体的分布函数。要了解总体的情况，就要了解随机变量x的分布或它的某些数字特征。样本是总体的代表和反映，简单随机样本应该能很好地反映总体的情况。那末，如何由样本来推断总体的分布呢?一般做法是作出样本分布函数用以观察理论分布的概貌。为此我们给出样本分布函数的定义。3

设(X1，X2，…，Xn)是来自总体X的一个简单随机样本，将其一个观测值(x1，x2，…xn，)的分量按从小到大的顺序排列成

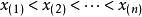
其中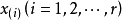 出现的频数为 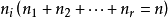，记

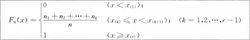
称F(X)为总体X的样本分布函数或经验分布函数。1

样本分布函数的图象意义样本分布函数的图像也是类似于离散型随机变量分布函数的图像，是一条跳跃式上升的阶梯形曲线，在每个间断点x(k)处跳跃。若样本观测值的各分量x1，x2，…，xn不重复，则每一跃度为 ；若某一分量重复m次，则在该分量处跃度为 。

性质由此定义容易看出，Fn(x)满足下列性质：

(1)(单调有界性)样本分布函数是单调增加的有界函数，且0≤Fn(x)≤1；

(2)(规范性) ， ；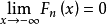

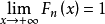(3)(右连续性)对于任意的实数a， ；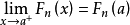

(4)Fn(x)为非减函数；

由此可见，样本分布函数Fn(x)具有分布函数的性质，我们可以将其看成是以等概率 取值X1，X2，…，Xn的离散型随机变量的分布函数。1

此外，对于任何实数x，Fn*(x)的值等于样本的n个观测值中不超过x的个数除以样本容量n。它正是n次独立观测中，事件{X≤x}出现的频率。由概率与频率的关系可知，当n充分大时，Fn*(x)可以作为未知分布函数F(x)的一个近似。因此样本分布函数Fn*(x)可以作为总体分布函数的近似，n越大，近似程度越好.这正是我们用样本观测值来估计和推断总体的一个重要依据。3

推论根据贝努力大数定理，只要n足够大，Fn(x)依概率收敛于总体分布函数F(x)。事实上还可以有更进一步的结论，这就是格利文科(w．Glivenko)定理

按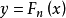 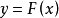， ，的图形，如下图，Cn，C来讲，这定理表明，对于任意给定的ε>0，概率为1时有：

当n足够大时，Cn的图形在用不等式

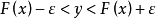
所定的带状区域内。

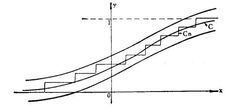
这些结论与下列直观事实相吻合。在某种灯泡的寿命总体中，随机地抽取一容量为20的样本及一容量为120的样本，其样本分布函数F20(x)及F120(x)的图形都是台阶形折线。可以看出，对不同容量的样本，其样本分布函数也不相同，但都是总体分布函数F(x)的缩影。由此可见，样本分布函数Fn(x)是总体分布函数F(x)的一个良好近似。2

格利文科定理说明了，当n充分大时，格里文科定理深刻地描述了总体X的样本分布函数Fn(x)近似于总体X的分布函数F(x)。因此对于较大的样本，样本分布函数Fn(x)可以作为总体分布函数F(x)的一个很好的近似．这是数理统计学中一切统计推断都用样本来估计和推断总体的理论依据。1

举例例1从一批标准重量为5009的罐头中，随机抽取8听，测得误差如下(单位；g)：8，一4，6，一7，一2，1，0，1，求经验分布函数，并作出图形。

解：将样本值按大小顺序排列为：一7