[科普中国]-数值方程

基本介绍

数值方程是量的数值间的关系式。由于量的数值与量所采用的单位有关，所以数值方程的形式与其中量所采用的单位有关。而且，在给出数值方程时，必须指明其中各个量所采用的单位。2

关于数值的详细说明见下文小节。

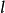举例说明在速度 ；长度 和时间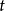 之间的量方程为：

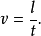
当采用km/h；m和s分别作为速度；长度和时间的单位时，导出的数值方程为：

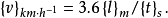这个式子的含义是：当长度以m作为单位的数值除以时间以s作为单位的数值所得之商，必须乘以3.6后才是以km/h作为单位的速度数值。

上述数值方程可写成：

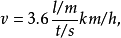但不可写成：

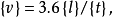也不应写成：

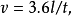因为上述第一种写法，虽有花括号说明是数值，但却未指明单位；上述第二种写法，这些量的符号是量？还是数？是不明确的。

但是，在工程技术界，大量地存在上述的第二种写法。

例如：

以盐酸标准滴定溶液作滴定剂测定某一物质的碱度，该盐酸标准滴定溶液确定了的浓度为c(HCI)=0.2 mol/L。其结果以氢氧化钾(KOH)的质量分数表示，其计算方法为：

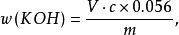式中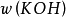：为KOH的质量分数，以%为单位；

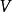为所消耗盐酸标准滴定溶液的体积，mL；

c(HCl)为盐酸标准滴定溶液的浓度，mol/L；

m为试料的质量，g；

0.056为氢氧化钾的摩尔质量，即M(KOH)，它等于0.056，以kg/mol为单位。

上述式子所用符号均为量的符号，但却只代表其量值中特定单位（在符号说明中指出）的数值，实际上是个数值方程。这个数值方程中所选用的单位，由于考虑到了等号左右单位的相等，在其形式上却完全与量方程一致。

等号左边的单位为：1；

等号右边的单位为：

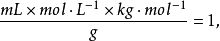因而未引入新的系数。2

数值的表达形式由于量A的量值表达为：

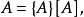其中：[A]为量A所采用的单位；而{A}则为采用[A]作为单位时A所具有的数值。因此，数值：

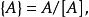这是数值的第一种表达式。

例如：

v/km·h：以公里每小时作为单位表达速度的数值；

c(H+)/mmol·L-1：以毫摩尔每升作为单位表达H+在溶液中的浓度的数值。

数值的第二种表达形式为：。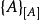

即以所采用的单位作为花括号的下标给出。这里，花括号已表达为一个数值，但必须交待的单位则作为下标。这种形式，同样是确切的。

例如：

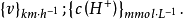由于第二种形式采用了下角标，在印刷上比较复杂，实际使用较少。

上述数值的表达形式的使用主要有以下三种场合：

a) 表格中的表头；

b) 坐标；

c) 数值方程。

关于数值的表达，不宜使用诸如：

a) 米数；

b) 摩尔数；

c) 安培数之类的形式。

因为上述三例中，米和摩尔固然只是用于表示长度和物质的量的单位而不致导致混淆，但安培数则既可用于表示电流，也可用于表示磁通势(按SI的规定，磁通势的SI单位也是安培)。

更不应将它们作为量的概念，例如：把物质的量称为摩尔数；把长度称为米数。2