[科普中国]-矩阵单位

在线性代数中，阶单位矩阵，是一个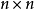的方形矩阵，其主对角线元素为1，其余元素为0。单位矩阵以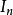表示；如果阶数可忽略，或可由前后文确定的话，也可简记为（或者E）。（在部分领域中，如量子力学，单位矩阵是以粗体字的1表示，否则无法与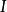作区别。）

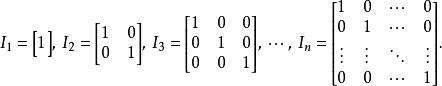
一些数学书籍使用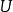和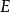（分别意为“单位矩阵”和“基本矩阵”），不过I更加普遍。

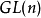特别是单位矩阵作为所有阶矩阵的环的单位，以及作为由所有阶可逆矩阵构成的一般线性群的单位元（单位矩阵明显可逆，单位矩阵乘自己，仍是单位矩阵）。

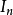这些阶矩阵经常表示来自维向量空间自己的线性变换，表示恒等函数，而不理会基。

有时使用这个记法简洁的描述对角线矩阵，写作：

也可以写作克罗内克尔δ记法：

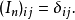
在数学中，克罗内克函数（又称克罗内克δ函数、克罗内克δ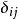）是一个二元函数，得名于德国数学家利奥波德·克罗内克。克罗内克函数的自变量（输入值）一般是两个整数，如果两者相等，则其输出值为1，否则为0。

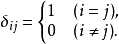
克罗内克函数的值一般简写为。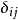

克罗内克函数和狄拉克δ函数都使用δ作为符号，但是克罗内克δ用的时候带两个下标，而狄拉克δ函数则只有一个变量。1

根据矩阵乘法的定义，单位矩阵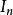的重要性质为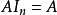：且。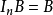

单位矩阵的特征值皆为1，任何向量都是单位矩阵的特征向量。具有重数。因为特征值之积等于行列式，所以单位矩阵的行列式为1。因为特征值之等于迹数，单位矩阵的迹为。2