[科普中国]-地铁卡中的数学

地铁卡中的数学

你知道吗，在小小的地铁卡中竟然也隐藏了诸多的数学问题，让我们一起来一探究竟吧。

一、地铁卡与黄金比

公交卡、地铁卡、银行卡，几乎每个上班族都有，它们的外形都是统一的圆角矩形。但你知道这个矩形的长宽比是多少吗？

这个比例就是所谓的黄金分割。把一条线段分为两份，使较短线段与较长线段的长度之比等于较长线段与整条线段的长度之比。那么这个比值就叫做黄金分割比（约为0.618），简称黄金分割。有趣的是，黄金比例的倒数正好比其大1。

人们认为，黄金分割这一比值能给人带来美感，因此常常应用于建筑、绘画、雕塑、音乐、摄影等领域。早在古希腊时代，人们就把黄金比例运用在了建筑和雕塑之中，例如建于公元前5世纪的帕特农神庙，其高与宽之比为19：31≈0.613，非常接近0.618；而由阿历山德罗斯创作的《断臂的维纳斯》，其肚脐的位置则恰为整个身体的黄金分割点。另外，埃及金字塔、巴黎圣母院、东方明珠等很多著名建筑中也有黄金比例的身影。

除此之外，黄金分割在管理、工程设计等方面也有着不可忽视的作用。例如，1953年，数学家基弗（Kiefer）利用黄金分割发明了优选法（又叫0.618法），通过尽可能少的试验次数找到生产和科学实验中最优方案。我国数学家华罗庚在晚年的时候深入工厂农村，推广和普及优选法，大大提高了生产效率。

其实，黄金比例在大自然中早就广泛存在了。例如，很多植物的叶子，相邻两片叶子之间的角度约为137.5°，这个角度把360°分成了两段，它们的比值恰好约为黄金分割比。植物学家经过计算认为：这个角度对叶子的采光、通风都是最佳的。

二、地铁卡中信息多

每天，成千上万的人进出地铁，伴随着闸机上一晃而过的余额——-2.32、4.00、68.31、237.50…。你是否思考过，这些余额蕴含着持卡人的什么信息？

以上海地铁为例，余额为3.00、4.00、5.00等小额整数的，大多是一次性地铁票，也就意味着持卡人很可能不在本地生活，而是来这里办事或旅游的。

另外，有的余额可以从心理学的层面，分析出一些信息。例如，如果余额很小甚至为负（上海地铁允许乘客欠一次费），持卡人多半是一个精打细算的慢性子；而如果余额较大（如600），则持卡人可能就是一个性格直爽的急性子。

最后，在一些特定条件下，通过地铁卡的余额，也许能从数学的角度分析出持卡人的乘车情况。举个例子，假设某地的地铁卡乘车费用统一为3.8元（打9折优惠），充值金额统一为整百元。此时，充值金额与最小非负余额存在以下对应关系：

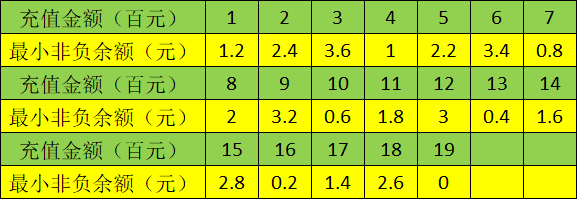
如果某人的地铁卡余额为55.8元，通过推算，其最小正余额为2.6元（55.8÷3.8=14.……2.6），通过上表，可以看出其充值金额至少为1800元，已使用金额为1800-55.8=1744.2元，已搭乘次数为744.2÷3.8=459次。而由于每充值1900元，余额就会循环一次，因此实际搭乘次数可能是1900n/3.8+459=500n+459次（n=0,1,2,3…）。如果假设持卡人每天搭乘两次地铁，则其在此地至少生活了250n+229.5天，就算n=0，也有半年以上了。

有人问，这点信息有什么用？在信息爆炸的今天，的确用处不大。不过笔者期待，某位侦探小说家，在读了这篇文章之后，写出一个故事——“地铁卡余额巧破案”，必定与众不同。

三、“双卡双待”不靠谱

2014年12月28日，北京地铁统一涨价，彻底告别2元低价时代：

有人提出一种“双卡双待”式的省钱攻略，希望通过巧妙的统筹安排，“合法逃票”。具体做法是，购买两张地铁卡，在第一次进站时同时刷两张卡（记为A、B卡），出站时只刷A卡。第二次进站时刷A卡进站，B卡出站。第三次进站时则刷B卡进站，A卡出站。此后，A、B卡交替着刷，一张卡进站，另一张卡出站。这样进站和出站会被记录为同一地铁站，因此扣费也总是按最低费用3元。

那么，这一方式真的有效吗？

北京法制晚报的记者亲自测试了这一“省钱妙招”，发现一旦地铁卡隔夜之后，就会被锁定，不能正常使用，需要乘务员解锁之后才能使用。相关人员表示，这一方式在短时间内是可以使用的，但在限时系统上线后，就不能奏效了。因为如果出站不刷卡结账的话，第二天进站会按最高金额扣费的。

现如今，各地的地铁站均有限时政策，规定乘客必须在数小时之内出站。一方面，是为了规避乞讨等长时间逗留的非正常行为；另一方面，则是为了规避这种“双卡双待”的“合法逃票”行为。

参考资料：

1.黄金比例.

2.网传两卡循环刷乘地铁省钱 记者核实隔夜就失效.法制晚报