[科普中国]-从“平行线”相交开始说起

当你在欣赏达·芬奇（Leonardo di ser Piero da Vinci）《最后的晚餐》时，除了惊叹作者巧妙的布局和精湛的画艺之外，有注意到画中的那些“平行线”吗？它们与现实生活中的平行线是一样的吗？

如图1所示，当我们将画面中的一些“平行线”延长过后，它们都相交于一点。

图1[1]：列奥纳多·达·芬奇《最后的晚餐》

等等，怎么感觉不对，我们在小学就学过：在同一平面内，永不相交（也永不重合）的两条直线叫做平行线。生活中的这些平行线在画中怎么会相交？

要回答这个问题，我们得从透视法开始讲起。

一、透视法的历史脉络

早在古希腊罗马时期的绘画中，就可以看到一些透视思想。到了中世纪，阿拉伯光学家阿尔哈曾（Alhazen）在实验中证明光能够以数学方式来表达，这为透视法的产生打下了理论基础。以乔托（Giotto）为代表的中世纪画家在创作中运用一种简易透视法，笔下的对象有“近大远小”等特征。然而，根据这种透视法创作出来的作品看起来并不协调，换句话说，既不够真也不够美。

到了文艺复兴时期，画家们发现传统的做法（近大远小等）已经行不通，甚至在一定程度上约束了他们的创作。怎样才能将景物完美地呈现出来？怎样更好地在二维的平面上描绘现实中的三维景物？为此，他们提出了线性透视法。

布鲁内莱斯基（ Filippo Brunelleschi）创立了线性透视法，他发现了线性透视法中“灭点”的概念以及一些法则；马萨乔(Masaccio)率先将这一透视理论用于实际绘画中，创作出《三位一体》；阿尔贝蒂（Alberti）在《论绘画》中第一次系统阐释线性透视法；弗朗西斯卡（Francesc）进一步发展了线性透视法理论……

什么是线性透视法？它的基本原理是什么？我们可以借助图2来理解。

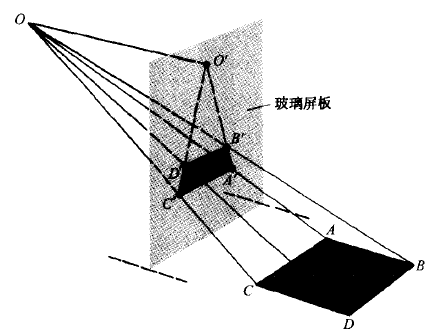
图2[2]

画家将自己的画布想象为一块玻璃屏板，通过它，他们能看到所要画的景物（矩形ABCD）。从一只认为是固定不动的眼睛（O）出发，设想光线能投射到景物中的每一点。这样的一束光线称为射影线（OA、OB等）。在这些光线穿过玻璃屏板（画布）之处都标出一个点。这样的点的集合就称为一个截景A′B′C′D′。

这一截景给眼睛的印象，与景物自身产生的效果相似。换句话说，就是将眼睛看景物时投影在插入其间的玻璃屏板上物体的大小、位置及其相互关系，在画布上表现出来。

他们还认为，需要安排画布上的一些平行直线（或延长后的直线）在某处相交，这样才使得作品更加符合我们眼睛所看到的样貌。于是，他们提出线性透视法的三条基本定理：

第一：“景物中所有与画布所在平面垂直的水平线，在画布上画出时都必须相交于主没影点（图2中点P，或称无穷远点）。”就是说AA´、BB´、CC´、DD´等线段都相交于P。

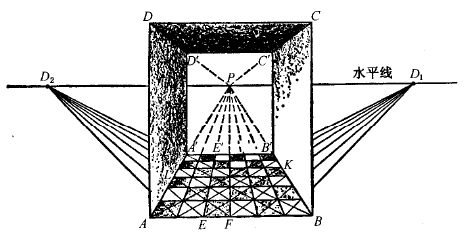
图3[3]：按照聚焦透视体系所画出的过道

达·芬奇等画家正是在创作中运用了这一定理，使生活中两条或多条平行线在画中神奇地相交！

其实，这一定理恰恰是符合我们眼睛看到的真实情况的。正如M·克莱因所说：“在透视学研究中产生的第一个思想是，人所触觉到的世界与人所看到的世界，这两者有一定的区别。相应地，应该有两种几何学，一种是触觉几何学，一种是视觉几何学。欧式几何是触觉几何学，因为它与我们的触觉一致，但与我们的视觉却并非总是一致。”想象一下，当你站在笔直的公路向远处看时，你会发现无限延长的两条路边在远处仿佛合成一条了！

第二：“任何与画布所在平面不垂直的平行线束，画出来时应该与其垂直的平行线相交成一定的角度，以便收敛于地平线上的一点。”如图中的D1、D2两点就是多条线束分别相交的点。第三：“景物中与画布所在平面平行的平行水平线，画出来时也将是水平平行的。” 如AB和DC、AD、BC。

我们在拉斐尔（Raffaello Santi）的作品（图4）中也能看到这种线性透视法基本定理的运用。

图4[4]：拉斐尔《雅典学院》

但是，这种透视法还是有明显缺点：我们平时是用两只眼睛去观察，而且每只眼睛看到的东西并不是完全一样的；另外，光线射在视网膜上是呈曲面形状的，并不是一块平面的底板。

二、射影几何的诞生

在研究线性透视法时，阿尔贝蒂提出了一个问题：“任意两个截景之间有什么样的数学关系？”（见图1）这一问题引起了德扎格（Desargues）的关注。这一原本为画家提供帮助的投射、截影的方法，因为它与锥面之间的特殊联系，被德扎格用于圆锥曲线的研究，并创立了一门新科学——射影几何！

1636年，德扎格出版了《关于透视绘图的一般方法》，这本只有12页的小册子宣告了他的射影思想的诞生。然而，他的这一小册子却没引起同时代人的重视，因为当时学界更多地是关注笛卡尔的新几何思想，即用代数方法处理几何问题。

1639年，他出版了《试论锥面截一平面所得结果的初稿》一书，却只发行了50本左右，他将这些分送给了朋友。法国数学界的一些人士看到后感到惊讶，甚至对德扎格进行敌意的攻击，这影响了德扎格的信心，于是他换了一种新的做法——通过他的朋友去传播。

1648年，他的学生，同时也是他的朋友博斯（Abraham Bosse）出版了《运用德扎格透视法的一般讲解》一书，其中介绍了德扎格的一些定理，最著名的便是“德扎格定理”，见图5：

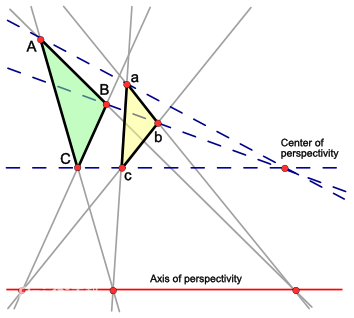
图5[5]

如图5所示，从透视中心（Center of perspectivity）这一点望过去的两个三角形，它们之间的对应边AB与ab、BC与bc，以及AC与ac的延长线相交的3个交点，必定在同一条透视轴（Axis of perspectivity）上。反之，如果两个三角形的三对对应边相交于同一条透视轴上，则连接对应顶点的三根连线必定相交于透视点。这一定理对于三角形ABC与abc在或不在同一平面都成立。

欧式几何一个很重要的特点就是将直线的相交与平行分开对待，但在德扎格这里发生了革命性的变化，他引入了无穷远直线和无穷远点，欧氏几何是回避这些的。而对于射影几何来说，平行线也会相交的思想是非常重要的，是射影几何理论大厦的根基。在德扎格之后，笛卡尔、帕斯卡等人相继投身于射影几何的研究，分别发现了笛卡尔定理、帕斯卡定理等，在数学界产生深远影响。德扎格则被认为是“第一位以精确的数学方式正确控制无限的概念的数学家。”

三、科学与艺术的二重奏

画家们在进行创作的过程中产生了关于投影截景的概念，从而创造出一套透视理论体系；数学家从这一思想出发，开辟了一个全新的领域：射影几何。正如M·克莱因所说：“17世纪最富独创性的数学成果，来自受绘画艺术的激发而产生的灵感……画家们在发展聚焦透视体系的过程中，引入了新的几何思想，而且提出了一系列导致这一研究进入全新方面的问题。通过这一方式，艺术家们‘偿还’了他们利用数学方法、思想而‘拖欠’数学的‘债务’。”

这让我们看到科学与艺术二者之间的关系不是对立，也不是简单交叉，而是在各自或相同的领域里追求共同的目标，都表现了大致相同性，这种相同性便是追求真与美的统一。

“科学史之父”萨顿（George Sarton）曾将分别对应于“真”、“善”、“美”的科学、宗教与艺术比喻为一个三棱锥塔的三面，并认为“当人们站在塔的不同侧面的底部时，他们之间相距很远，但当他们爬到塔的高处时，他们之间的距离就近多了。”也就是说，随着人类认识的不断进步，我们最终会在最高点达到真、善、美的统一。

如爱因斯坦所言，画家、诗人、思辨哲学家和自然科学家都总是用各自最适当的方式去描绘简化和容易领悟的世界图像。从乔托到布鲁内莱斯基，从阿尔贝蒂到达·芬奇，最终到德扎格，世界图像的真与美在他们那里相遇、碰撞和重构！

注释：

①出自https://baike.baidu.com/item/最后的晚餐/572?. 图中黑线为本文作者所加.

②出自M·克莱因著;张理京,张锦炎,江泽涵译.古今数学思想（第一册）[M].上海:上海科学技术出版社,2002:P335.

③出自M·克莱因著,张祖贵译.西方文化中的数学[M].上海:复旦大学出版社, 2005:P136.

④出自https://baike.baidu.com/item/雅典学院.图中黑线为本文作者所加。

⑤出自https://en.wikipedia.org/wiki/Desargues%27_theorem.

主要参考文献：

1、戴吾三,刘兵编.艺术与科学读本[M].上海:上海交通大学出版社,2008.

2、M·克莱因著,张祖贵译.西方文化中的数学[M].上海:复旦大学出版社, 2005.

3、M·克莱因著,张理京,张锦炎,江泽涵译.古今数学思想（第一册）[M].上海:上海科学技术出版社,2002.

4、乔治·桑塔亚纳著,张旭春译.艺术中的理性[M].北京:北京大学出版社,2014.

5、王哲然.透视法的起源[M].北京:商务印书馆,2019.

6、https://en.wikipedia.org/wiki/Girard_Desargues.

7、https://en.wikipedia.org/wiki/Desargues%27_theorem..