[科普中国]-众所周知，数学是一门好吃的学科

自古以来，食物不仅仅是人类物质和能量的来源，同时也是一门高深的学问。作为探寻人类与食物之间关系的一门学问，美食学（Gastronomy）本身便是一门多元的学科，其中蕴含了医学、农学、化学、生物、地理，也包括历史、哲学、人类学、心理学、社会学，而大家都喜闻乐见的数学，也与美食有着密不可分的关系。

数学作为一种极富创造力的学科，从某种意义上来说本身就具有艺术的属性，数学之美与美食之美更是相得益彰。为了让更多读者（吃货）意识到数学的魅力，今天我们就带大家探寻数学中的美食秘籍，为大家揭秘舌尖上的数学。

《中华小当家》中，钢棍解师傅就已经懂得运用黄金分割制作烧麦。

思考题：图中AQ：AB = ？

图片来源：动漫《中华小当家》

快餐：三明治vs汉堡

美食并不一定需要华丽的摆盘以及繁琐的步骤，日常的美食也可以十分美味，就譬如快餐的代表三明治。三明治备受数学家喜爱，譬如下面这个定理，就被称作“三明治定理”：

机智的读者们可能已经发现，这其实就是大学微积分开篇就会提到的夹逼定理或者夹挤定理。而之所以叫它三明治定理，因为三明治形象地表达了这个定理被“夹”起来的特点。

米奇精湛的刀工，保证了两片面包片的极限相同，因而两片面包之间的面包片的极限也相同

图片来源：《米奇与魔豆》

当然，三明治不可能只有面包，根据三明治的官方定义，它是一种在面包中间放置肉、奶酪或蔬菜等食物，加上调味料、酱汁任意搭配在一起的小吃。因此也就有了下面的定理——火腿三明治定理。[1]

在n-维空间中有n个可测的“物体”（紧集，即闭合且有界的集合），可以用一个(n？1)-维的超平面把它们同时分成测度相等的两部分。

要理解这条定理，首先需要澄清几个名词：

· 测度：简单而言，所谓测度就是把集合映射到非负实数，以此来定义这个集合的大小。严格的数学定义如下：

· 集合X的σ-代数：又称为X的σ-域，是X的幂集（包含所有X的子集的集合系）的子集合。

· 超平面：指n-维欧几里得空间中，余维度是1的子空间，或者说是n-维空间中的(n？1)-维子空间。例如平面中的直线，空间中的平面。

火腿三明治定理可以视为博苏克-乌拉姆定理（任何一个从n-维球面到欧几里得n-维空间的连续函数，都一定把某一对对跖点映射到同一个点）的一个推论。运用到三明治上，即在三维空间中的3个可测的紧集（火腿三明治 =面包+火腿+面包），可以用一个(3？1)-维的超平面（刀片）把它们同时分成测度相等的两部分。

图片来源：《卫宫家今天的饭》

当然，快餐的选择当然不是只有三明治一种，爱吃汉堡的小伙伴也可以在数学中找到自己的最爱——Hamburger moment problem

图片来源：《蜡笔小新》

Hamburger moment problem即Hamburger矩问题，其中的Hamburger指的是德国数学家Hans Ludwig Hamburger（所以这个定理和我们吃的汉堡包好像没啥关系）。要理解这个问题，首先要理解“矩”的含义。moment在某些物理学文献中译作“动差”，用来表示物体的形状。实数域上的连续实函数f(x)相对于实数c的n阶矩定义为mn，

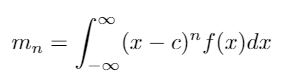
但实际上矩在概率学领域也应用十分普遍。聪明的读者可能已经发现，如果令c = 0，n = 1，取f(x)为概率密度函数，则f(x)相对于值0的1阶矩等于连续随机变量的数学期望：

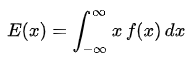
进一步，令c = E(x)，改变n的值，我们有：

· n = 2，m2定义了方差

· n = 3，m3定义了偏态

· n = 4，m4定义了峰态

而所谓的“矩问题”，指的是能有通过一个测度μ的矩序列mn确定该测度。其中

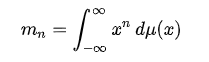
根据μ的支撑集的不同， 矩问题出现了三个比较有名的“变种”[2]：

· Hamburger 矩问题：μ的支撑集为(？∞, +∞)

· Stieltjes 矩问题：μ的支撑集为 [0,+∞)

· Hausdorff 矩问题：μ的支撑集为有界闭区间

与其他的矩问题类似，Hamburger矩问题的关键在于μ的矩序列的存在性、唯一性以及其结构（即如何描述μ的集合），文献[2]对此有详细的解释。

正餐：披萨牛羊大龙虾

有时候食客们选择快餐并非是出于口味上的偏好，而是别无选择之下的无奈之举。下面就让我们一起走进卖相相对更好（价钱相对更高）的料理，同时发掘其背后隐藏的数学奥秘。

图片来源：《海贼王》

披萨因为可以与大家一起分享，因此成为一种在全世界都颇受欢迎的食物。然而，经常吃披萨的小伙伴们往往会遇到一个难题：如何才能分到更多的披萨？平面几何学中的披萨定理或许可以解决这个难题[3-4]。披萨定理指出，如果以披萨上任意一个指定点为中心，切下n刀，使相邻的两刀隔的角度相同；然后按某个方向顺次为切出的各块交替染上两种颜色，那么有：

· 当有任意一刀通过圆心或n是大于2的偶数时，两种颜色的面积一样大。

· 如果任意一刀都不通过圆心，那么：

n 当 n = 1 或 2，或者n除以4余3时，包含圆心的部分比较大

n 当n大于4且除以4余1时，不包含圆心的部分比较大

图片来源：自制

这个定理可以说明，当两个人在分披萨的时候，如何才能拿到更多。披萨定理的证明并不困难，也没有用到太多超出微积分领域的知识，但步骤之繁琐却远超笔者的想象（甚至可以单独写一篇文章来论述）。下面提供一个n = 4的特例下，不需要公式的证明，定理的完整证明请参见[4]。

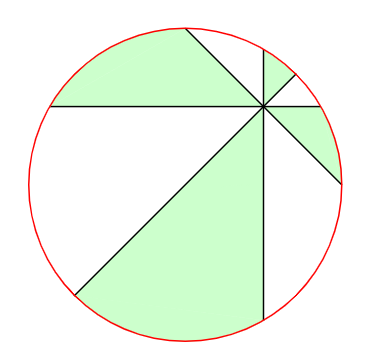
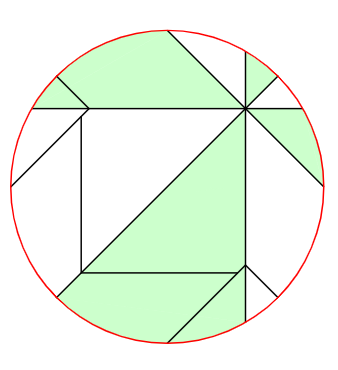
上图为n = 4，即一张披萨切4刀的情况。证明思路基本可以总结为东拼西凑。显然，阴影部分面积和空白部分面积相等。

图片来源：自制

当然除了披萨之外，牛羊肉也是必不可少的经典美食。显然数学对于牛羊的研究也从未停止过，例如小学数学经典问题“牛/羊吃草”问题。不过，今天我们要分享的是另一个经典“牛/羊/马吃草”问题。

图片来源：《小羊肖恩》

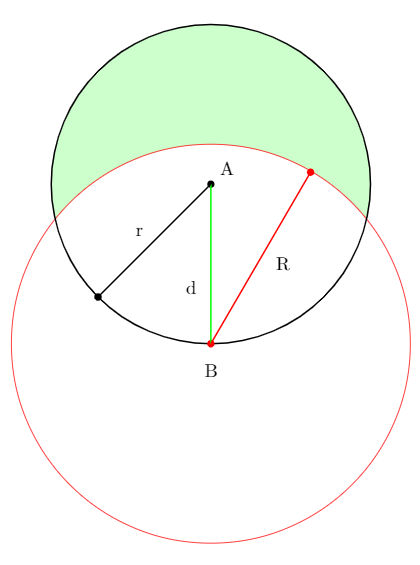
图片来源：自制

图中有一片圆形的草场，圆心为A，半径为r。在草场边缘有一点B，拴着一匹羊（当然如果你喜欢吃牛肉的话就可以栓一头牛）。栓羊的绳子长为R。问当R多长时，才能让羊在草场的一半区域吃草？

这道题最直接的思路是利用微积分求解。不过如果我们可以引入方程

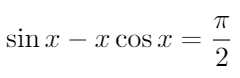
的解x = 1.9056957293…，我们就完全可以借助初中的知识解答这道题。

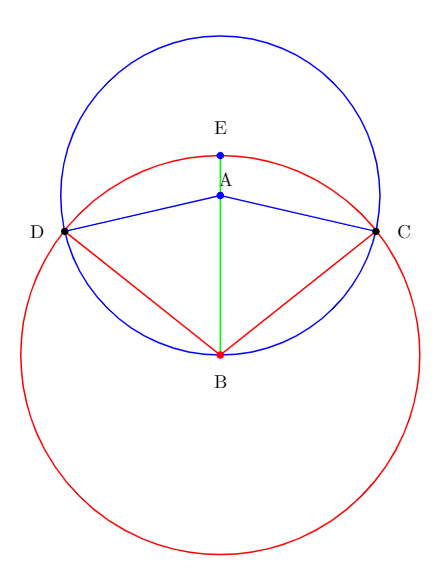
图片来源：自制

不失一般性，这里我们假设草场半径r = 1，同时定义以下符号

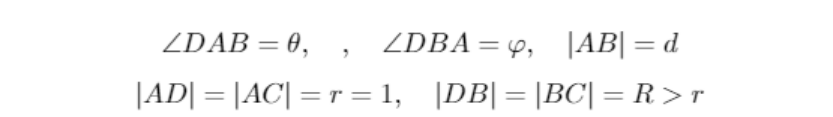
根据余弦定理可知，

同理

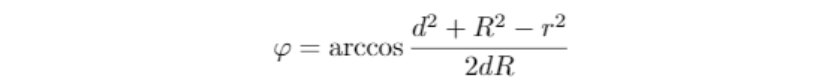
利用小学的几何知识，我们可以很轻易地计算出

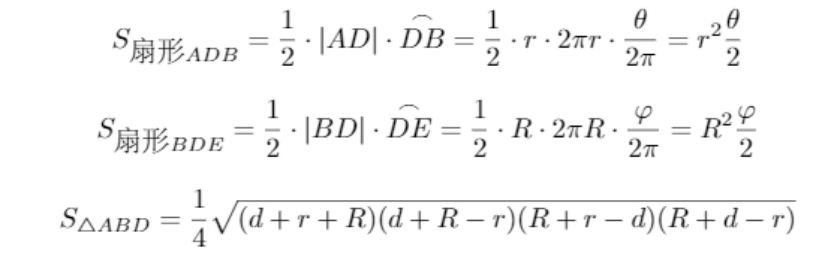
将前述的表达式代入

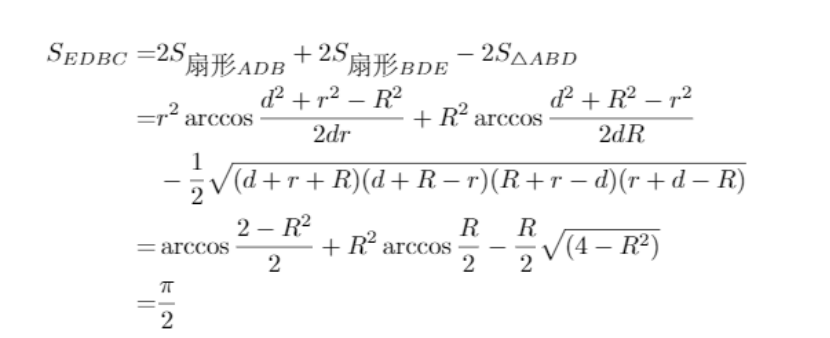
令SEDBC = 半个草场的面积 = pi/2，解出R的值即可。这里的问题最终归结为在[0, pi]的范围内求解

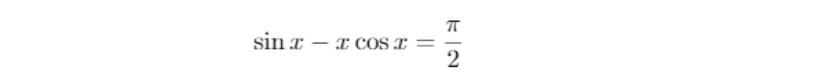
也算是唯一超纲的知识点。

用了这个定理，就能让牛羊在变成美食之前，更加茁壮地成长了。

图片来源：《小羊肖恩》

除了上述食材，海鲜中也有不少美味的食材，譬如接下来我们要介绍的龙虾。龙虾是节肢动物门软甲纲十足目龙虾科下物种的通称，因其味道鲜美而广受大家喜爱。

图片来源：《食戟之灵》

在图论中，有一类特殊的“树”就被称为“龙虾图”。要了解龙虾图，首先需要理解“图”和“树”两个概念。

· 图：在图论中，图用于表示物件与物件之间的关系。一张图由顶点（或结点）以及连结这些点的边组成。可以将图G定义为由顶点集V与边集E组成的二元数对 (V, E)。如果给图的每条边规定一个方向，那么得到的图称为有向图。相反，边没有方向的图称为无向图。

· 树是一种无向图，其中任意两个顶点间存在唯一一条路径。

对于一棵树而言，我们可以选其中的一个顶点，并称之为树的根。这样我们就定义了有根树：

一个有根的树叫做有根树

为了方便起见，我们同时给出以下定义：

· 一条边的两个端点中，靠近根的那个节点叫做另一个节点的父节点。

· 两个端点中距离根比较远的那个节点叫做另一个节点的子节点。

· 没有子节点的子节点叫做叶节点。

· 与某个顶点相关联的边数的总和称为这个顶点的度。

有了上述名词，我们就可以定义以下两种图：

· 毛虫图（毛虫树），指的是图的每一个顶点或者在中心轴上，或者距离中心轴只有一条边。树是毛虫图，当且仅当所有大于等于3度的节点被至多两个大于等于2度的节点包围。

· 龙虾图（龙虾树），指的是移除叶节点会留下毛虫图的图。因为形状酷似龙虾，因此有了这个名字。

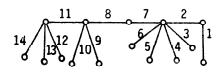
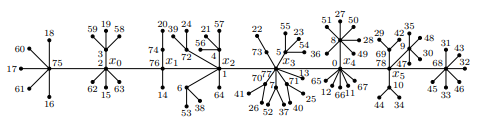
数学家眼中的毛毛虫（上）vs 数学家眼中的龙虾（下）

图片来源：[5-6]

小食：奶冻香蕉麦乐鸡

吃完正餐，餐后的小食甜品也是必不可少的。首先为大家介绍的便是著名的法式甜点——奶冻（blancmange）。

图片来源：giphy

上面魔性的动图恰好也体现了法式奶冻的一个重要特点，自相似性。根据这一特性，我们可以推测法式奶冻本身应该具有分型结构。1901年，类域论的开创者高木贞治给出了一个函数[7]

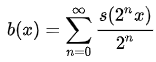
其中s(x)为三角波函数，定义为

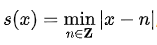
这就是著名的法式奶冻曲线。

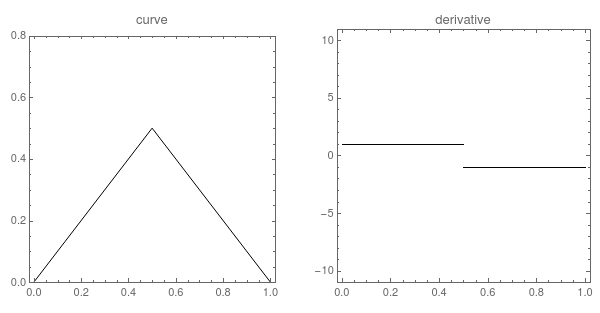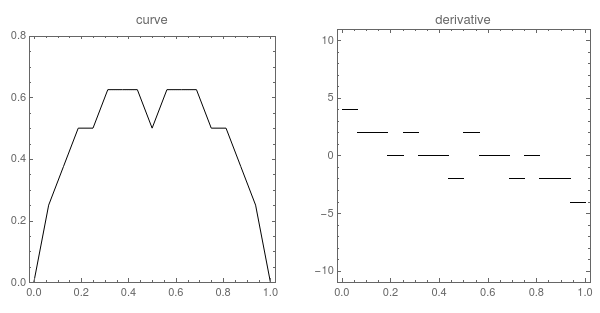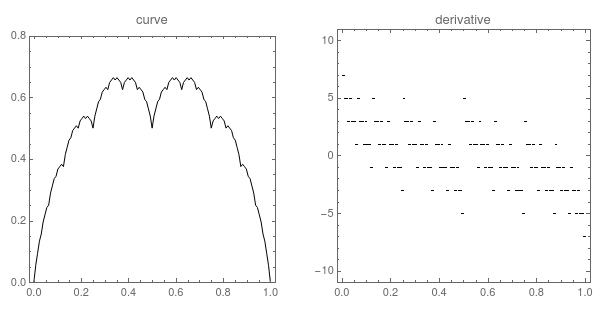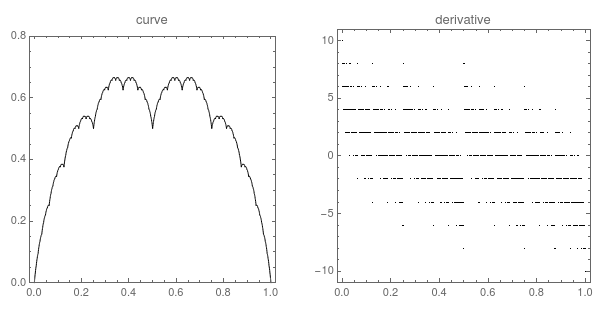
法式奶冻曲线，顾名思义，就是长得跟法式奶冻一样的曲线。与其他分型函数一样，法式奶冻曲线是一种处处连续，但又处处不可微的函数图形。

图片来源：自制

传统上法式奶冻用牛奶或鲜奶油加糖制成，同时加入杏仁增添风味。不过改良后的甜品可以通过加入草莓、香蕉或其他水果来增加风味。说到香蕉，它是芭蕉科芭蕉属植物，不少美味的甜点都离不开香蕉。

图片来源：《卑鄙的我》

在数学中，不时也可以看到香蕉的身影。例如在数学优化理论中，Rosenbrock函数又被人们称为“Rosenbrock香蕉函数”，常被人们用来测试最优化算法的性能。Rosenbrock函数被定义为[8]

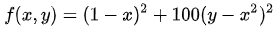
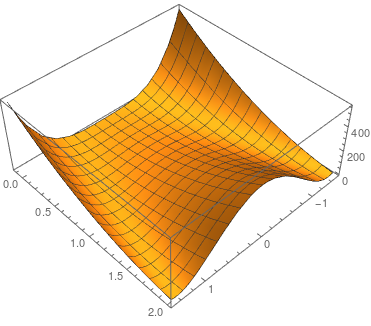
图片来源：自制

函数的等高线大致呈抛物线形，其全局最小值位于香蕉型的山谷中。这个点其实很容易通过肉眼发现，但由于山谷内的值变化不大，要通过算法找到这个最小值还是有些难度的。

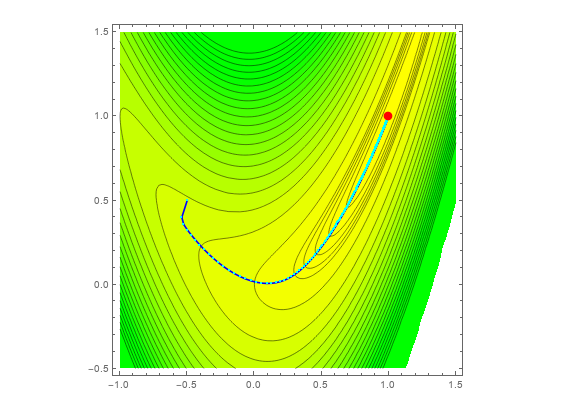
利用Rosenbrock函数测试梯度下降法。其中红点表示全局最小值f(x,y) = 0，此时(x,y) = (1,1)。

图片来源：自制

说罢香甜可口的点心，咸香酥脆的小吃也颇受人们喜爱，譬如麦乐鸡。

麦乐鸡的蘸酱都有不少粉丝

图片来源：《瑞克和莫蒂》

在数学上，硬币问题（又称Frobenius 硬币问题）有一个变种，被称为“麦乐鸡（McNugget）数问题”[9]，也从侧面反映了麦乐鸡的强大影响力。

硬币问题是指求仅使用特定面额的硬币无法获得的最大金额。例如，3元硬币和5元硬币无法获得的最大金额是7元（所以几乎没有什么中央银行会发行3元硬币）。这里要求硬币面额的最大公约数为1。用数学语言可以描述为，已知正整数a1，a2，……，an且 (a1，a2，……，an) = 1。则对于正整数集合{k1，k2，……，kn}，求k1a1 + k2a2 + ··· + knan可以组成的数字中最大的那一个。

硬币问题的一个变种就是所谓的麦乐鸡数问题。已知麦当劳售卖的麦乐鸡有三种规格：6块装、9块装和20块装（这里不考虑“开心乐园餐”里包含的4块装麦乐鸡），可以用上述三种规格麦乐鸡组成的麦乐鸡块数都被称为麦乐鸡数。麦乐鸡数问题指的是求出最大的非麦乐鸡数，即不能用上述三种规格的麦乐鸡组成的鸡块数。

如果深究下去，麦乐鸡数问题还有很多角度的性质有待发掘。譬如最大的非麦乐鸡数的存在性问题，麦乐鸡规格数增加对最大非麦乐鸡数的影响等等。不过对于眼前这个问题，我们可以用十分直观的方式来解决。

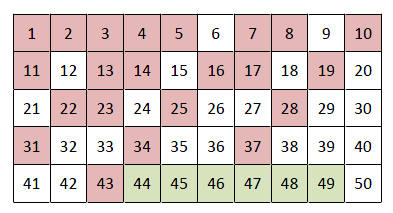
图片来源：自制

上图中，红色标记的数字是非麦乐鸡数，注意44~49，这六个相连的数字都是麦乐鸡数，所以保证了大于44的数都是麦乐鸡数。因此最大的非麦乐鸡数为43，即点餐时麦乐鸡块数超过43，就一定可以用若干盒6块装、9块装和20块装麦乐鸡组成。

数学与美食一样，伴随人类走过了漫长的岁月。美食之美，唯有品尝过后才能体会；数学之妙，恐怕也只有走进之后方能发觉。愿诸位看完这则短文，也能体会数学与美食的共通之处。美食不可辜负，数学亦复如是。

参考文献：

[1] Beyer, W. A., Zardecki, Andrew (2004), The early history of the ham sandwich theorem, American Mathematical Monthly, 111 (1): 58–61.

[2] Chihara, T.S. (1978), An Introduction to Orthogonal Polynomials, Gordon and Breach, Science Publishers.

[3] Upton, L. J. Problem 660. Mathematical Magazine. 1967, 40: 163.

[4] Mabry, R. and P. Deiermann (2009). Of Cheese and Crust: A Proof of the Pizza Conjecture and Other Tasty Results. American Mathematical Monthly. 116: 423–438.

[5] Harary, F. and Schwenk, A. J (1973). The Number of Caterpillars. Disc. Math. 6, 359-365.

[6] Mishra, D., Panigrahi, P. (2016). Some new classes of graceful Lobsters obtained from diameter four trees. Mathematica Bohemica, Vol. 135 (2010), No. 3, 257-278.

[7] Takagi, Teiji (1901), A Simple Example of the Continuous Function without Derivative, Proc. Phys.-Math. Soc. Jpn., 1: 176–177.

[8] Rosenbrock, H.H. (1960). An automatic method for finding the greatest or least value of a function. The Computer Journal. 3 (3): 175–184.

[9] Wah, Anita; Picciotto, Henri (1994). Lesson 5.8 Building-block Numbers. Algebra: Themes, Tools, Concepts. p. 186.