[科普中国]-真空不空？声音还可以在其中传播？

上周，12月11日，《自然》杂志报道了一项足以撕掉全世界物理课本的研究：声音能够在真空里传播！

我们初中的物理课本说：声音的传播是需要介质的，所以真空中是无法传播声音的。

到高中之后，我们的物理书又进一步解释道：声音的本质是物质分子的振动所引起的一种波，因为真空是空的，当然也就没有物质分子的振动，所以振动的声波就传不过去。

实验事实是不会错的，那么我们的教科书错了吗？

其实在上面这段话里，我们“理所应当”地认为真空是全空的。但是，在量子世界里，没有任何事情是理所应当的。

那么，真空里到底有什么？这和声音在真空中传播有什么关系？

别急，我们马上就来说一说关于“真空不空”的故事。在这个故事里，我们将会看到，真空里的东西不但能传播声音，还是让壁虎能够趴在墙上的原因，更是大名鼎鼎的霍金辐射（也称黑洞辐射）的源头。

1.弹簧与小球：量子场论的缘起

约100年前，人们已经知道，原子中的电子如果吸收能量，那么自己的能量就会升高；如果想跳回原来的状态，必须要通过释放一份电磁波的形式来释放能量，这份波被爱因斯坦称为光子。

这个现象就好比人如果吃了葡萄皮，那么他可以吐出一个葡萄皮，比较平淡无奇。

但人们还发现，有时电子不用吸收能量，也会主动释放光子，这一现象叫做自发发射。这就类似一个人没有吃葡萄皮，但是也能吐葡萄皮，这个现象就比较诡异。

1927年，物理学的一代宗师狄拉克给出了一个解释。他认为：真空中虽然看起来没有葡萄也没有葡萄皮，但这只是表面现象。真空中存在着许多的“葡萄-葡萄皮”组成的对子，它们产生得很快，消失得也很快，差不多同时发生，使得真空表现得像是没有葡萄一样。

现在假想一个“葡萄-葡萄皮”对子出现在你嘴边，此时恰好葡萄掉进了你的嘴里，于是你吸收了一个葡萄，而真空中就剩下了一个葡萄皮。所以看起来就好像你虽然没吃任何东西却吐了一个葡萄皮一样，只不过这个葡萄是真空投喂给你的，我们只观察到了剩下的皮而已。

玻尔曾说：“在所有的物理学家中，狄拉克拥有最纯洁的灵魂。”狄拉克坚持认为物理方程应该拥有完美的数学形式，并以此信条来指导自己的研究。对于“丑陋”数学的拒绝使他后来的研究逐渐偏离了主流。图为1930年前后的狄拉克。（图片来源：维基百科）

这一假说由于完美解释了自发发射而获得了成功。经过一系列修正和重塑（尤以杨振宁教授的大师之作——杨-米尔斯理论最为重要）之后，这套理论发展为后来的量子场论。

其主要观点也很简单：首先，对于任何物质（或能量）来说，都有一个与之对应的“场”，例如光子对应电磁场，电子对应电子场。场可以看作是由许多被弹簧连着的小球组成的，每个场都充满着整个空间。

注释：如何理解此处的“任何”二字呢？这里的任何是可以在字面意义上来理解的。例如，对象对应着对象场，头发对应着头发场。按照量子场论，真空中电磁场涨落能够产生光子，电子场涨落可以创造电子，对象场的涨落是可以创生出对象的，而头发场的涨落是可以创造头发的。先别高兴得太早——物质越大，产生的概率就越小。连电子产生的概率都已经无限接近于零了，就不要妄想获得头发和对象了。

图片来源于新浪微博

然后，由于弹簧的存在，所以每个小球都在不停振动，科学家称之为“涨落”。如果这个振动太剧烈使得弹簧被拉断，那么就会得到自由的小球。例如，电子场的涨落可以产生一个电子。

水波的涨落可以偶尔产生一个水珠，而这个水珠又快速落回水波里，场的涨落产生粒子的过程与此类似。（图片来源：http://bostonreview.net/books-ideas/matthew-buckley-search-new-physics-cern-part-2）

最后，自由小球重新回到小球阵列中。自由小球不断地从空间中快速产生又消失，从而使得空间中整体而言不存自由的小球，维持一个整体的平衡。

2.卡西米尔效应

每个新理论出现之后，科学家总是急于寻找验证它的方法。

1948年，荷兰理论物理学家卡西米尔通过纯理论计算找到了一种验证上述理论的方法，这就是著名的卡西米尔效应。

设想有一个大的真空空间，其中有两个平行金属板。由于两板之间的空间相对于板外来说比较小，因此如果量子场论是正确的，那么板间的场里含有的小球数应该少于板外空间。那么，板间的小球对板的撞击力应该小于板外小球对板的撞击力，所以板会受到外界的挤压力。

很快，这一理论预测的现象就被观测到了。在真空中的平行金属板受到了真空施加的挤压力。

也就是说，真空里确实有很多小球！真空不是空的！

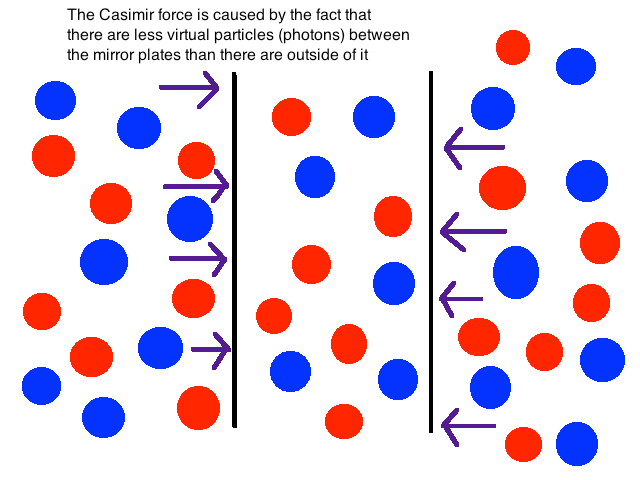
由于板间的场涨落产生的粒子少，因此会感受到外面空间产生的压力，这就是卡西米尔效应。（图片来源：https://skepticalinquirer.wordpress.com/2015/08/05/casimir-effectefek）

根据狭义相对论，物质和能量的本质是一样的，真空中有很多小球，就意味着真空中有不为零的能量。科学家能够计算出真空中能量的数值，称之为零点能。

可不要小看零点能哦，虽然平时我们感受不到它的作用，但是当两个金属板距离很近的时候（例如10纳米左右），真空零点能能够在金属板上施加约1个大气压的压强。因此在高级计算机芯片或者航天器设计过程中，必须考虑卡西米尔效应的影响。

3.声音穿过了真空

量子场论认为，所有的物质和能量都可以对应一个真空中的场，那么声音作为一种振动能量，也可以对应一个振动能量的场。

让我们再次考虑两个真空中的平行金属板，它们之间存在上述的振动能量场。如果在一个板上施加振动能量，这个能量会和板间的振动能量场发生交互，从而引起另一片金属板的振动，这便是声音的卡西米尔效应。也就是说，声音可以通过真空传播。在微观层面上，分子振动也是一种热现象，因此声音能穿过真空而传播，也就意味着热量也可以跨越真空而传播。

注释：热量传递的方式有热传导、热对流和热辐射，其中传导和对流是需要介质的，辐射不需要介质，但是能量是以电磁波的形式传播的。本实验中证明的热量跨越真空传播，并非通过辐射形式而传播，是真正意义上的热量不需要介质而传播。

虽然理论上可以预测该效应，但是由于它十分微弱，所以观测是很困难的。加州大学伯克利分校的Zhang lab在巧妙设计的实验装置的帮助下，首次观测到了声音在真空中传播的现象，也即本文开头处所提到的研究成果。

这再次证明了量子场论的主要观点：“真空不空”和“万物皆场”****。

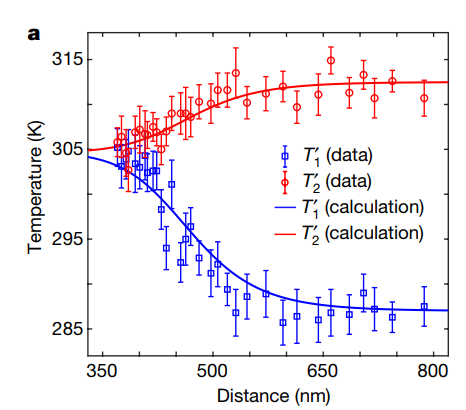
当两个金属板间的距离小于500纳米时，能够观察到高温物体的温度（T2）减小而低温物体的温度（T1）增加，也就是说热量（振动能量，也就是声音的能量）跨越了真空而传播。实验排除了对流和辐射的干扰。

（图片来源：参考文献1）

4.黑洞与壁虎

为什么霍金说黑洞会发出辐射？壁虎又为什么能够挂在墙上？这都跟我们今天讲的量子场论和卡西米尔效应有关。

霍金利用真空不空的原理预言了黑洞辐射的存在。

他的主要观点为：黑洞是一种光速都无法逃离其引力的天体。我们考虑黑洞边缘的空间，由于场的涨落，有可能产生一对正反物质小球。由于量子力学的测不准原理，这对小球的速度有可能超过光速。此时若反物质小球落入黑洞，那么正物质小球就有可能挣脱黑洞的束缚而飞出。落入黑洞的反物质小球和黑洞内其它的正物质小球重新结合而使得黑洞的质量减少。那么总的结果就是：黑洞质量减少，同时放出了一个正物质小球。这就是黑洞辐射的原理。

该理论打破了人们印象中黑洞“只进不出”的形象，具有划时代的意义，也是霍金的史诗级成果之一。

注释：关于超光速的问题，狭义相对论只是论证了“物体无法通过加速的方式达到光速”，但并未限制物体诞生时的速度可以超过光速。否则的话，连光本身也不能达到光速了。

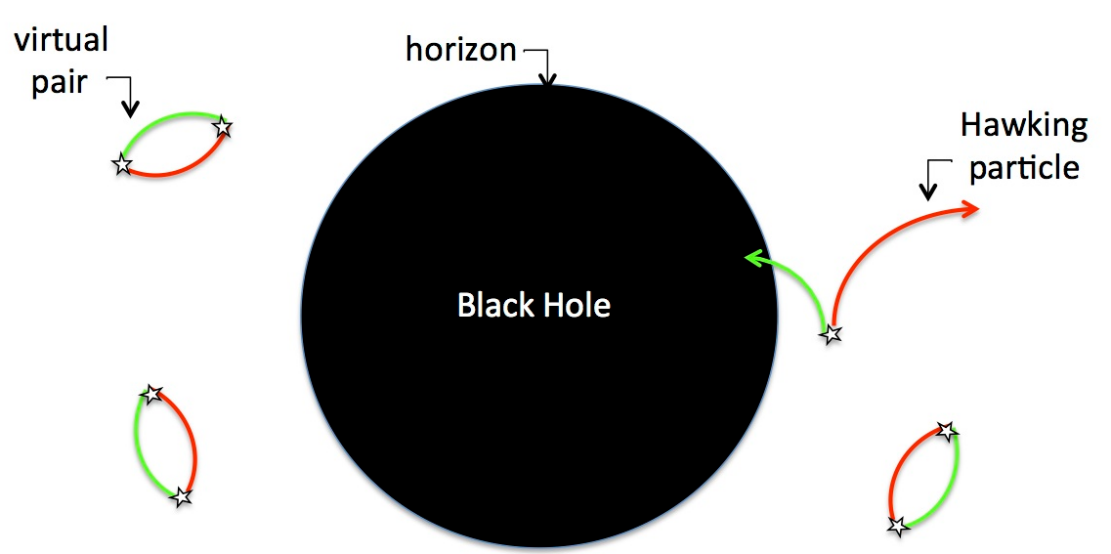
如图，成对出现的粒子中，如果有一个落入黑洞而另一个逃离黑洞，逃离的那个粒子就成为黑洞辐射。(图片来源：https://www.physics-astronomy.org/2017/04/physicists-created-black-hole-in-lab.html)

更让人意想不到的是，小小的壁虎竟然也能够利用卡西米尔效应来爬墙。

壁虎的脚上有数万根刚毛，每一根都极其细小，小到每根刚毛和墙壁间的距离都只有纳米级。前面我们提到过，如果两个板的间距很小，那么卡西米尔效应可以施加非常可观的压力将两个板压在一起。所以，壁虎脚上的数万组卡西米尔效应将它挂在墙上。

注释：通常，壁虎爬墙被解释为是由于刚毛和墙壁之间的范德华力。范德华力是卡西米尔效应的微观角度描述，是分子尺度的卡西米尔效应，二者等价。

壁虎脚上数纳米大小的帽状结构，为壁虎提供了足够的卡西米尔效应力。(图片来源：https://www.pinterest.com/pin/238761217724719845/?lp=true)

壁虎虽然不懂量子场论，但伟大的自然界却是无所不知的。在美丽而又精妙的自然界面前，无人敢称全知，无人敢称伟大。

注释：为方便理解，本文对复杂的概念在不影响正确性的基础上进行了具象或简化处理，若需获得详细的解释，请咨询专门人士或后台联系作者。

参考文献：

Fong, K.Y., Li, H., Zhao, R. et al. (2019). Phonon heat transfer across a vacuum through quantum fluctuations. Nature 576, 243–247

Nikoli？, Hrvoje (10 October 2016). Proof that Casimir force does not originate from vacuum energy. Physics Letters B. 761: 197–202.

Spagnolo, S. (2007). Casimir-Polder interatomic potential between two atoms at finite temperature and in the presence of boundary conditions. Physical Review A. 76 (4): 042112.