[科普中国]-让学生头疼的公式原来这么美

1**）纳维-斯托克斯方程式：**

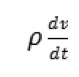
（矢量形式）

纳维-斯托克斯方程是以克劳德-路易·纳维和乔治·斯托克斯命名，广泛应用于流体物质的方程。流体，其实简单说就是流动的物体，比如空气和液体。通过依赖微分方程的形式来描述流体的运动，并不是普通的代数方程，纳维-斯托克斯方程所表示的是一个变化的过程，正如没有绝对静止的流体。

为什么说这个方程式美呢？这又不得不回到它的描述对象，流体。举个最简单的例子，水。水美不美，集刚柔于一身，既有“海神东过恶风来，浪打天门石壁开”这等气势磅礴，亦有“柔情似水,佳期如梦,忍顾鹊桥归路。两情若是久长时,又岂在朝朝暮暮”这般缠绵入骨。

除了诗人的文采，难道大家就不好奇都是水，到底它们内在的差别是什么？纳维-斯托克斯方程便是这条发现之路不可缺少的指南针。最后附一张流体电镜图。

2**）吉布斯自由能**

能够拿诺贝尔化学奖的分支里怎么能少得了物理学呢，作为一个在热力学中出现的重要参数G(吉布斯自由能)，其为化学反应的研究发展产生了深远的影响，其发现者吉布斯是一位完全配得上诺贝尔化学奖的数学物理学教授！

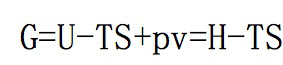
吉布斯方程

有了吉布斯自由能，我们可以判断一个化学反应能否发生，甚至可以预测什么条件下发生。一般来说当吉布斯自由能小于零的时，反应能够自发发生，而大于零时则会发生副反应。我们可以举一个简单的例子。

假设一个反应焓变为274，熵变为1，此时在0摄氏度的条件下，我们可以计算出吉布斯自由能为：

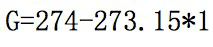
结论是大于零的。这是反应无法自发发生。

而为了反应能够自发发生，我们能够做些什么呢？升高温度！现在假设我们在100摄氏度下做同样的反应会怎么样呢，此时，

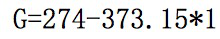
结论G约为-100，此时反应就正常自发发生了。

吉布斯方程的理论在理论上为化学化工生产提供了指导性意见，通过计算，我们能够知道是否反应，怎么反应，如果不反应如何进行改进让其容易反应。

3**）阿伦尼乌斯方程**

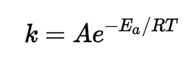或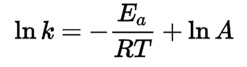

阿伦尼乌斯方程是最早由范特霍夫提出，瑞典科学家阿伦尼乌斯进一步分析得到的温度和反应速率的关系，并且提出能垒Ea的存在。

我认为整个方程最精华的地方在于提出了能垒这个概念，也就是说，Ea不变的情况下，无论如何改变外界条件,比如温度浓度等，反应都不会发生。

能垒在自然界中是普遍存在的现象，大部分的非自发反应都需要从外界获取能量以跨越能垒使反应能够得以发生。很多化学反应的条件十分苛刻，原因就在于能垒极高，反应想要发生需要汲取天地日月之精华（从外界获得极高的能量）

就好像你无法得到心仪姑娘的心一样，条件不过硬，说啥都白扯，你们之间的化学反应就是没法发生。那么我们有什么办法降低反应的能垒也就是Ea呢？答案是长得帅（催化剂）。

科学家们开发出各种各样的催化剂，让Ea变得更低，使得以前在较为温和的条件下无法发生的反应现在可以发生。阿伦尼乌斯方程导出了能垒的概念，加深了我们对化学反应的理解，在药物合成，化工生产，材料研究中应用极广。

生物学是充满了个体不确定性的研究科目，尤其是基础生物类都是寻找现象解释机理，缺乏像数学和物理那样准确的定量描述。并且生物本身是没有什么所谓的生物公式，基本就是统计学由来，物理学由来或者微积分的简单公式。

该公式的名字极具后现代意识流风格，其背后的故事更是令人莞尔乃至惋惜。1908年，当时供职于都柏林健力士酿酒厂的统计学家戈斯特发表了t检验的相关论文。该检验完美的契合了酿酒厂对于产品质检的需求，并马上在工程及科研领域得到广泛应用。然而，工厂老板认为该公式的发明人属于商业机密，戈斯特最终被迫使用笔名“学生”（student）来命名这一公式，从而失去了一个名垂史册的机会。

用t分布理论来推论差异发生的概率，从而比较两个平均数的差异是否显著。研究里最常用的显著性水平是0.05，0.01。也就是说，当科研工作人员得出实验组和比较组显著水平小于0.05时，就可以高举双手欢呼：是的！看我有了多么了不起的世界级新发现！

当然，有时候我们在论文里写道，我们以其中几个为样本进行了深入的研究，其实潜台词非常可能是，如果再加两个样本或更多，显著水平就会大于0.05，就变得毫无意义了。。。。。。

4） 范德华状态方程

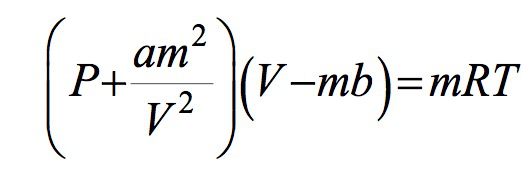
关于理想气体有几个假设:气体分子不占空间，一直作直线运动，撞在容器壁上不发生变化，像弹力球一样回弹，此外分子间没有任何关系，都是孤独的分子，也不会变成液体或固体。

而1873年物理学家范德华（Johannes van der Waals）提出了实际气体状态方程。其特点在于将被理想气体所忽略的气体分子自身体积和分子间作用力考虑在内了。自此对气体的宏观物理特性有了更精确的描述。

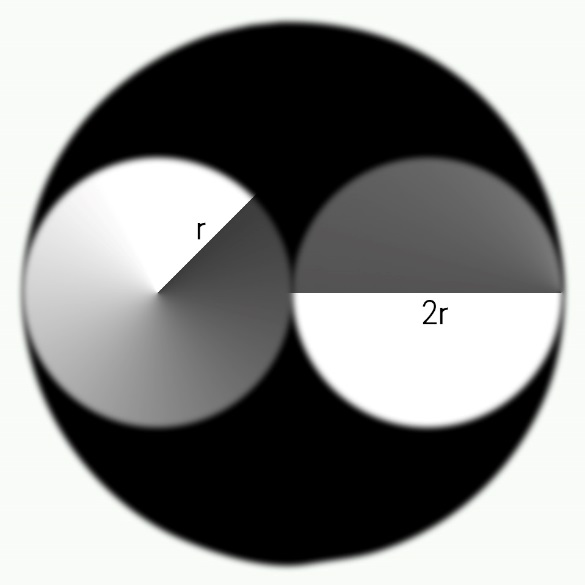
a. 水分子之间的范德华力 b. 一个双原分子的排斥体积

这个公式为什么牛呢，它是人类历史上第一个既能反映气、液各相性质，又能描述相变和临界现象的状态方程。它描述了热力学系统平衡状态的独立参量与温度之间的关系。由于形式简单，物理意义清楚，这个方程成为了热力学和统计物理学的追捧对象。

范德华描述方程中分子间作用力时所使用的研究方法实际上就是后来所说的平均场方法，这一方法对铁磁、超导、超流等众多物理系统相变和临界现象的研究，对热力学和统计物理理论的发展产生过重大影响。

5） 塔珀自指公式

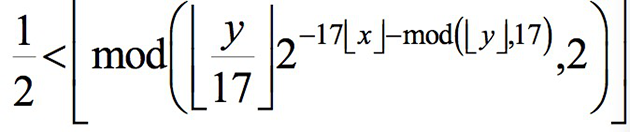
塔珀自指公式是杰夫·塔珀（Jeff Tupper）发现的自指公式。其中， mod表示模除。奇妙的是公式的二维图像与公式本身外观一模一样，由于这个公式很有代表性，又比较有趣，在很多数学、计算机科学课程里被用作绘制公式图像的练习作业。如果取一个常数k，让它等于：

960 939 379 918 958 884 971 672 962 127 852 754 715 004 339 660

129 306 651 505 519 271 702 802 395 266 424 689 642 842 174 350 718 121 267 153 782 770 623 355 993 237 280 874 144 307 891 325 963 941 337 723 487 857 735 749 823 926 629 715 517 173 716 995 165 232 890 538 221 612 403 238 855 866 184 013 235 585 136 048 828 693 337 902 491 454 229 288 667 081 096 184 496 091 705 183 454 067 827 731 551 705 405 381 627 380 967 602 565 625 016 981 482 083 418 783 163 849 115 590 225 610 003 652 351 370 343 874 461 848 378 737 238 198 224 849 863 465 033 159 410 054 974 700 593 138 339 226 497 249 461 751 545 728 366 702 369 745 461 014 655 997 933 798 537 483 143 786 841 806 593 422 227 898 388 722 980 000 748 404 719

此公式的二维图像

这个公式本身是一个从常数k中解码出一个相对应的黑白位图的通用方法，所以事实上它可以用来绘制任何图像。

这块无穷大的位图中有一个横向切片描绘了绘制函数自身，但这并不意外，因为别的切片会描绘所有能被填进17像素高的位图中的公式。

塔珀（Jeff Tupper）还通过电子邮件传播了这个原始公式的扩展版本，这些版本的公式把其他的切片都抹除了。这里的常数k是把公式的单色位图化成二进制后乘以17得来的。如果把k除以17（并化成二进制），最小一位代表图像左下角的像素；最小的17位就构成了最左边的一列像素；第二小的17位构成了左数第二列像素；以此类推。很神奇吧？

6） 曼德博集合

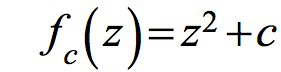
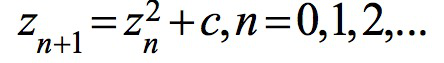
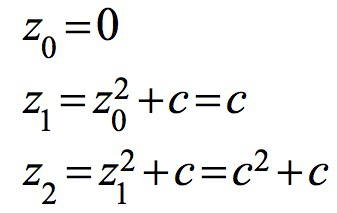
每次迭代的值依序如下面序列所示：

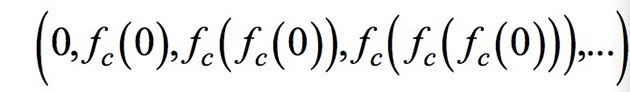
不同的参数c可能会让序列的绝对值逐渐发散到无限大，也可能收敛在有限的区域里。曼德博集合M就是让序列不延伸到无限大的所有复数c的小分队。

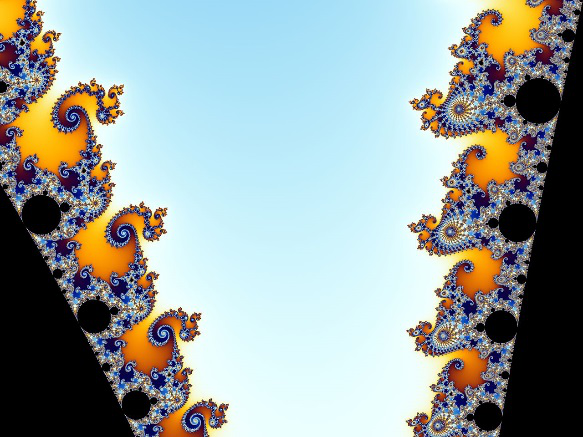
图为曼德博集合

如果我们把复数c表示成复平面上的点，在这个平面上，曼德博集合就是分形的人大代表。

上图中后一个图像是前面图像的局部放大。分形图可以无限重复，无数的圆圈围绕包括原点在内的心形，把无数较小的圆圈限定到圆。

另外，如果放大周围环境，可以发现周围环境形状和这个分形图非常相似。如果把我们每个人想象成其中的一份子，很多“我们”形成了体积更大的“我们”，没有尽头，没有终点，无限循环，想来是不是挺可怕的？

**7)**魏尔斯特拉斯函数

这可能是因为直观上想象一个连续但在不可数个点上不可导的函数是很困难的事。当我们绘制函数的图像时，总会画出较为规则的图形，比如满足利普希茨条件的函数图像。

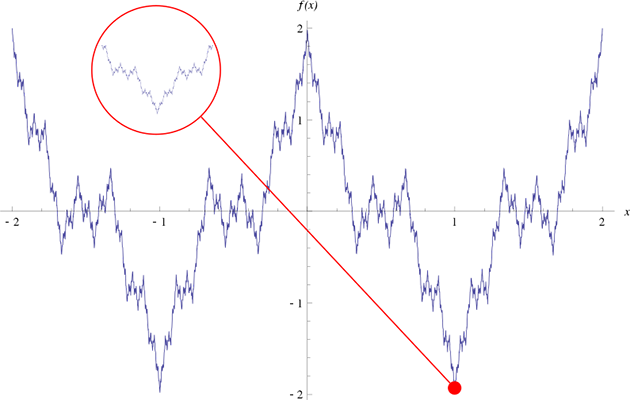
图为区间[−2, 2]上的魏尔斯特拉斯函数。这个函数具有分形特性：某些部分会和整体自相似。

魏尔斯特拉斯函数可以被看作第一个分形函数，尽管这个名词当时还不存在。无论如何放大，函数图像都不会显得更加光滑，也不存在单调的区间。把魏尔斯特拉斯函数在任何一点放大，得到的局部图都和整体图形相似。这个函数和上面的曼德博集合类似，“你的身体的任何一小部分都是另一个你自己！

**8)**质能方程

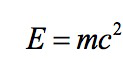
这个方程极其简单，没有复杂的运算关系，看起来有一种简洁的美感。如果现代物理学的理论都能像这个公式这么简单，那所有搞物理的人都应该放下手中的工作庆祝三天三夜，而他们之所以没能停下手中的工作来庆祝，就是为了实现这样的目标！

物理学是为了看透复杂世界背后的简单本质。公式中，E代表的是能量，m代表的是质量，c代表的是真空中的光速，这个公式表明任何有质量的物体都具有能量，反之亦然。

以后胖的人可以自豪的说，质能方程表明，质量大的人具有更大的能量，而且是正比于光速的平方增长的哦。这一方程是爱因斯坦在奇迹年也就是1905年的一篇论文中写下的，是从狭义相对论中得到的。质能方程表明，静止的有质量的物体也具有内禀能量，是静止能量，当它动起来时，除了静止能量，还有动能，静止能量和动能之和是总的能量，这样换算出的质量就会变大，也就是动质量会大于静质量。

核武器以及核电站利用的核能，以及我们的太阳能，都是是原子核在发生反应时由于微小的质量亏损而释放出的巨大能量，原子弹和核电站是利用重核裂变；太阳内部是轻核的聚变；科学家们一直致力于在地球上实现可控核聚变，一劳永逸地解决能源问题。既然是等式，转换就是双向的，宇宙大爆炸初期是没有物质存在的，高能光子的碰撞产生了轻子夸克等粒子，宇宙逐渐冷却才形成现在的物质。

**9)**万有引力定律

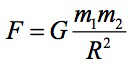
万有引力定律可以说是最为著名的物理定律了。艾萨克·牛顿其在1687年出版的《自然哲学的数学原理》中，详细阐述了其三大运动定律和万有引力定律，该书的原文使用拉丁文写成的。

读过该书的人会知道，该书远非我们所知晓的一些定律这么简单。本书可以说是科学研究的典范，在引论部分先给出定义、公理或运动定律，接下来三部分就是论物体的运动两卷和论宇宙的系统。

牛顿在该书中详细推导了在引力作用下的三种轨道即椭圆、双曲线和抛物线，里面所用到的几何学的知识和技巧，即使是现代人，也很难想到。而且在《原理》一书中，可以看出牛顿已经应用了微积分的思想，而他关于微积分的详细论述则在其他数学著作中。

传说牛顿是在苹果树下被苹果砸中受启发而发现万有引力定律，现在剑桥三一学院以及剑桥大学植物园内还保留着这棵苹果树的后裔，中国科学院上海分院还嫁接了一枝。万有引力定律将地上的苹果落地现象、大海的潮汐以及天上日月星辰的运动统一了起来，表明任何两个有质量的物体之间都存在引力作用。

虽然现在广义相对论是描述引力本质的理论，今年诺贝尔物理学奖发现的引力波也再次证明广义相对论的正确性，但并不代表万有引力定律的失效，宏观天体在引力作用下的运动用万有引力定律来解决，仍然十分方便和精确，而且在天文观测上也有很重要的意义。

1846年法国数学家和天文学家勒维耶根据引力定律计算得到一颗未知行星对天王星公转轨道的引力摄动，建议柏林天文台寻找这颗未知行星，结果找到了天王星，而且观测到的天王星的位置与勒维耶的计算结果只差1度，可以说明引力定律仍然是十分精确的和应用广泛的。另外，描述真空中点电荷的相互作用的库仑定律，也是类似的平方反比定律。平方反比这一关系，在很多其他情况下也应用广泛，是很好的近似。

10) 引力场方程

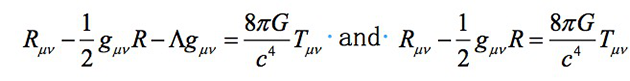
方程左边表示的是时空的弯曲情况，右边表示的是引力场作用下的物质及其运动，两边相等就表示了物质和时空的相互作用，用美国物理学家惠勒的话说就是“时空告诉物质如何运动，物质告诉时空如何弯曲”。