超球面,也称n维球面,是普通的球面在任意维度的推广。它是(n + 1)维空间内的n维流形。特别地,0维球面就是直线上的两个点,1维球面是平面上的圆,2维球面是三维空间内的普通球面。高于2维的球面有时称为超球面。
简介1.定义高于2维的球面称为超球面。中心位于原点且半径为单位长度的 维球面称为单位n维球面,记为
维球面称为单位n维球面,记为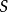 。用符号来表示,就是:
。用符号来表示,就是:
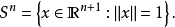 超球面是n维球体(
超球面是n维球体(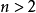 )的表面或边界,是
)的表面或边界,是 维流形的一种1。
维流形的一种1。
对于任何自然数 ,半径为
,半径为 的
的 维球面定义为
维球面定义为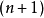 维欧几里得空间中到某个定点的距离等于常数
维欧几里得空间中到某个定点的距离等于常数 的所有点的集合,其中
的所有点的集合,其中 可以是任何正的实数。它是
可以是任何正的实数。它是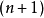 维空间内的
维空间内的 维流形。特别地:
维流形。特别地:
1) 0维球面是直线上的两个点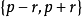 ;
;
2) 1维球面是平面上的圆;
3) 2维球面是三维空间内的普通球面;
4)3维球面是四维空间内的球面。
2.(n+1)维空间中的欧几里得坐标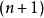 维空间中的点:
维空间中的点: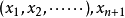 定义了一个
定义了一个 维球面
维球面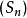 ,由以下方程表示:
,由以下方程表示:
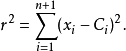 其中
其中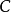 是中心点,
是中心点, 是半径。
是半径。
以上的 维球面在
维球面在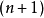 维空间中存在,是
维空间中存在,是 维流形的一个例子。半径为
维流形的一个例子。半径为 的
的 维球面的体积形式
维球面的体积形式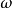 由下式给出:
由下式给出:
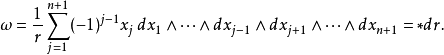 其中*是霍奇星算子。因此,
其中*是霍奇星算子。因此,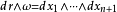 。
。
3.超球体由 维球面所包围的体积,称为
维球面所包围的体积,称为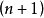 维球体。如果把球体的表面包括在内,则
维球体。如果把球体的表面包括在内,则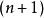 维球体是封闭的,否则是开放的。
维球体是封闭的,否则是开放的。
特别地:
1) 1维球体,是一个线段,是0维球面的内部。
2) 2维球体,是一个圆盘,是圆(1维球面)的内部。
3) 3维球体,是一个普通的球体,是球面(2维球面)的内部。
4) 4维球体,是3维球面的内部。
超球体的体积 维球面所包围的体积(
维球面所包围的体积( 维球体的体积)由以下公式给出:
维球体的体积)由以下公式给出:
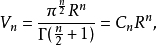 其中
其中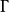 是伽玛函数。对于偶数
是伽玛函数。对于偶数 ,
,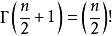 ;对于奇数
;对于奇数 ,
,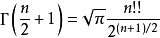 ,其中
,其中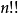 表示双阶乘。
表示双阶乘。
由此可以推出,对于给定的 ,常数
,常数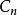 的值为:
的值为:
1)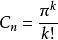 (对于偶数n=2k),
(对于偶数n=2k),
2)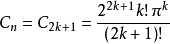 (对于奇数n=2k+1)。
(对于奇数n=2k+1)。
这个(n-1)维球面的表面积是:
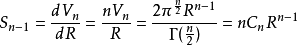 n维球面的表面积和体积之间有以下的关系:
n维球面的表面积和体积之间有以下的关系:
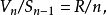
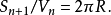 从此可以推导出递推关系:
从此可以推导出递推关系:
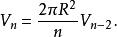 这些公式也可以直接从n维球坐标系中的积分推出。
这些公式也可以直接从n维球坐标系中的积分推出。
例子对于较小的 ,半径为
,半径为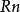 维球体的的体积
维球体的的体积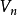 为如下:
为如下:
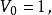
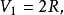
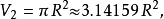
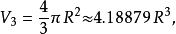
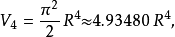
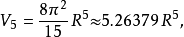
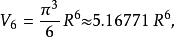
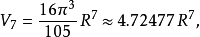
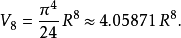 但当
但当 趋于无穷大时,
趋于无穷大时,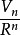 趋于0。
趋于0。
如果维度 不限于整数,那么
不限于整数,那么 维球面的体积就是
维球面的体积就是 的连续函数,它的极大值位于
的连续函数,它的极大值位于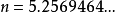 ,体积为
,体积为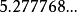 。当
。当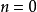 或
或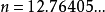 时,体积为1。
时,体积为1。
单位 维球面的外切超正方体的边长为2,因此体积为2;当维度增加时,
维球面的外切超正方体的边长为2,因此体积为2;当维度增加时, 维球面的体积与外切于它的超正方体的体积之比单调减少。
维球面的体积与外切于它的超正方体的体积之比单调减少。
超球坐标系可以定义 维空间内的坐标系统,与3维空间内的球坐标系类似,由径向坐标
维空间内的坐标系统,与3维空间内的球坐标系类似,由径向坐标 和
和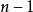 个角度坐标
个角度坐标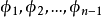 组成。如果
组成。如果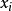 是笛卡儿坐标系,那么我们可以定义2:
是笛卡儿坐标系,那么我们可以定义2:
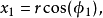
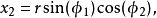
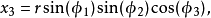
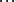
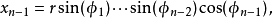
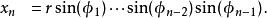 从中可以推出逆变换的公式:
从中可以推出逆变换的公式:
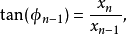
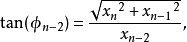
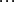
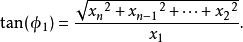 注意最后一个角
注意最后一个角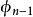 的值域为
的值域为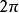 ,而其它角的值域为
,而其它角的值域为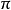 。这个值域覆盖了整个球面。
。这个值域覆盖了整个球面。
 维空间内的体积元素可以从变换的雅可比行列式得出:
维空间内的体积元素可以从变换的雅可比行列式得出:
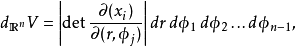
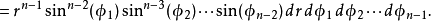 以上n维球体的体积方程可以通过积分来重新得出:
以上n维球体的体积方程可以通过积分来重新得出:

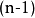 维球面的体积元素是2维球面的面积元素的推广,由以下公式给出:
维球面的体积元素是2维球面的面积元素的推广,由以下公式给出:

本词条内容贡献者为:
王海侠 - 副教授 - 南京理工大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国