[科普中国]-整数指数幂

形如ax的式子称为幂，其中a称为幂的底数，x称为幂的指数。当x取正整数，零，负整数时，ax分别称为正整数指数幂、零指数幂、负整数指数幂，统称为整数指数幂1。

基本介绍正整数指数幂一般地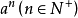， 叫作 的次幂， 叫作幂的底数， 叫作幂的指数，并且规定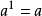 。我们注意到在 的n次幂定义中，n是正整数，因此通常又把它称为正整数指数幂2。

容易验证，正整数指数幂的运算满足如下法则：

(1) ；

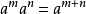(2) ；

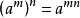(3) ；

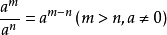(4) 。

负整数指数幂在法则(3)中规定了 ，如果取消这个限制，就需要讨论下面两种情形：

❶当 时，幂的商有如下运算：

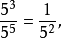依照法则(3)则有

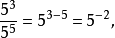即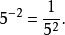

这就说明当指数为负整数时，幂的值是有意义的。此时规定

叫作负整数指数幂。

零指数幂❷当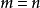 时，幂的商有如下运算：

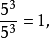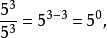且 故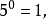

这说明当指数为零时，幂的值是有意义的。此时规定

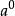叫作零指数幂，又叫零次幂。但是 是无意义的。

正整数指数幂、负整数指数幂、零指数幂统称为整数指数幂。正整数指数幂的运算法则对整数指数幂仍然是成立的。特别地，有2

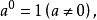
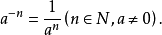
整数指数幂的运算法则同上所述，容易验证，正整数指数幂的运算满足如下法则：

(1) ；

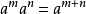(2) ；

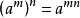(3) ；

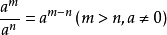(4) 。

(5)；

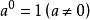**注：**①这些运算性质在整数指数范围内仍然适用。

②任何不等于零的数的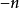 (n为正整数)次幂，等于这个数的n次幂的倒数，即 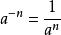( 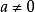，n为正整数)。在这两个幂的意义中，强调底数 都不等于零，否则无意义。

③学习了零指数幂和负整数指数幂后，正整数指数幂的运算性质可以推广到整数指数幕的范围3。

本词条内容贡献者为:

王海侠 - 副教授 - 南京理工大学