函数构造论中的主要研究课题,是由逼近论中正定理和逆定理两部分构成。正定理为由被逼近函数的构造性质推出逼近函数的逼近性质。逆定理为由逼近函数的逼近性质推出被逼近函数的构造性质。许多情况下,正定理和逆定理是一对互逆的命题。
简介函数构造论包括正逆两方面的定理。
所谓正定理就是从函数的结构性质(连续性、李普希茨条件、可微性等)来导出用n次多项式(或其他函数系)逼近函数时,其最佳逼近值(又称最佳逼近度)趋向于零的速度估计;
所谓逆定理就是用n次多项式(或其他函数系)逼近函数时,从其最佳逼近值趋向于零的速度估计式来导出函数本身的结构性质。因此,研究函数的结构性质就可以化归为研究用多项式(或其他函数系)逼近时,其最佳逼近值趋向于零的速度。
许多情况下,正定理和逆定理是一对互逆的命题。
函数逼近论[approximtion theory of functions]
研究如何用某些计算简单的函数(称为逼近函数)近似地表示一般函数(称为被过近函数) 的数学分支。通常逼近函数与被逼近函数属于某个线性赋范空间.对于有限区间[a,b] 上的函数.通常采用代数多项式和样条函数作过近函数,而对于周期函数,则采用三角多项式和样条函数来过近。
函数过近论的研究内容除可过近性、最佳逼近理论等属于一般逼近论范畴的问题外还有下列与函数有关的问题:
(1) 函数构造论。
(2) 线性算子逼近(approximation by liuear operators)。最佳逼近元虽然有最好的逼近度,但它是非线性的且计算复杂应用不方便。于是,人们构造了各种有较好逼近度的线性算子。对于周期函数,杰克逊算子
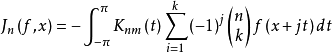 是比较理想的逼近工具,其中
是比较理想的逼近工具,其中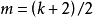 ,若 k 为偶数;
,若 k 为偶数; ,若 k 为奇数;且
,若 k 为奇数;且
 系数
系数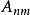 是使
是使 的规范常数。算子
的规范常数。算子 是
是 (n 阶三角多项式的全体的集)但线性算子,其逼近误差可用
(n 阶三角多项式的全体的集)但线性算子,其逼近误差可用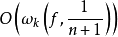 来估计。对于
来估计。对于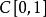 中的函数,最经典的算子为伯恩斯坦多项式算子
中的函数,最经典的算子为伯恩斯坦多项式算子
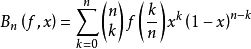 这是一个线性正算子。
这是一个线性正算子。
(3)插值逼近 (approximation by interpolation) 。设 f 是 上(连续或 k 次连续可微)但函数,
上(连续或 k 次连续可微)但函数, 是
是 上 n+1 个点,称为 插值节点,简称节点。插值逼近是指满足插值条件
上 n+1 个点,称为 插值节点,简称节点。插值逼近是指满足插值条件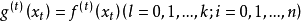 的逼近函数 g 来逼近 f 。通常,采用代数多项式、三角多项式、样条函数作为逼近函数。
的逼近函数 g 来逼近 f 。通常,采用代数多项式、三角多项式、样条函数作为逼近函数。
拉格朗插值多项式 (Lagrange interpolation polynonial) 是最简单的插值逼近工具。设 是
是 上的连续函数,
上的连续函数,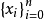 是插值节点,n 次代数多项式
是插值节点,n 次代数多项式

是满足 的唯一确定的 n 次代数多项式,称为 n 次拉格朗日插值多项式,其中
的唯一确定的 n 次代数多项式,称为 n 次拉格朗日插值多项式,其中

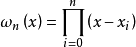
假如除了满足函数值的插值条件外还满足各类导数或高阶导数的插值条件就得到埃尔米特插值多项式。对周期函数可仿照代数多项式构造拉格朗日三角插值多项式。
(4) 有理函数逼近(approximation by rational functions)。有理函数是两个代数多项式之比,其中分母在所考虑的自变量区间内不等于零。在切比雪夫研究多项式逼近的同时也就已经考虑了有理函数的最佳逼近理论。但真正受到重视是在1964 年纽曼(D.J.Newman) 发现用 n 次有理丽数在 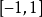 上通近丽数
上通近丽数  的过近度可以达到
的过近度可以达到  的惊人结果发表以后。许多与代数多项式逼近问题可对有理函数通近作平行的讨论。例如,关于有理逼近的正定理和逆定理也都已建立。
的惊人结果发表以后。许多与代数多项式逼近问题可对有理函数通近作平行的讨论。例如,关于有理逼近的正定理和逆定理也都已建立。
(5) 极值问题(extremum problem)。函数逼近论中出现大量的极值问题。除单个函数的最佳逼近外,人们还常常考虑计算最佳逼近在某个函数类中的上确界,计算线性算子逼近偏差关于函数类的主项。此外,还有宽度问题等。这些极值问题的解决有助于发现好的逼近工具。
(6) 复变函数逼近(approximation by function of complex variable)。研究用特殊的解析函数近似地表示复变函数的复分析的分支。逼近的可能性,逼近速度以及各种表示方法的研究构成了复变丽数巡近论的基本内容。常用的逼近工具有插值序列、正交多项式。法贝尔多项式、连分式、幂级数和指数多项式序列,狄利克雷级数等。许多问题可以与实变函数情况平行地提出。例如,借助多项式逼近和有理逼近中最佳逼近元的存在性唯一性以及特征刻画等。还有各种极值问题和偏差估计都是人们感兴趣的问题。1
本词条内容贡献者为:
王海侠 - 副教授 - 南京理工大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国