[科普中国]-触变性流体

定义

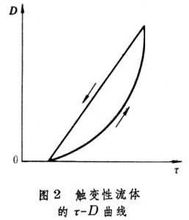某些流体的黏度不仅与切变速度大小有关，而且与系统遭受切变的时间长短有关，它们是时间依赖性流体。此种流体又可分为两类：①触变性(thixotropy)系统，②震凝性(rheopexy)系统。这两种系统都是非Newton流体，但切变与时间有关。前者维持流体以恒定切变速度流动的切力随时间而减小，后者在一定切变速度下，切力随时间而增加。

绝大多数时间依赖性流体是触变性流体(thixotropic fluid)。触变性流体内的质点间形成结构，流动时结构破坏，停止流动时结构恢复，但结构破坏与恢复都不是立即完成的，需要一定的时间，因此系统的流动性质有明显的时间依赖性。触变性可以看成是系统在恒温下“凝胶一溶胶”之间的相互转换过程的表现。更确切地说，物体在切力作用下产生变形，若黏度暂时性降低，则该物体即具有触变性。

产生触变性的原因并不十分清楚。如前所述，一种看法是认为针状和片状质点比球形质点易于表现出触变性，它们由于边或末端之间的相互吸引而形成结构，流动时结构被拆散，切力使质点定向流动。当切力停止时，被拆散的质点要靠Brown运动使颗粒末端或边相互碰撞才能重新建立结构，这个过程需要时间，因而表现出触变性。触变性是一个较为复杂的问题，许多现象尚不清楚，例如，石英粉的水悬浮液本来没有触变性，但加入一些极细的Al2O3粉末后即出现触变性，其原因就不明。1

在实际生产中有许多触变性问题，例如油漆和油墨的质量常决定于是否有良好的触变性。在刷油漆时，人们希望油漆的流动性要好，刷时省力，易于涂匀，且可使油漆光滑明亮。但是当刷子一离开，就要求油漆黏度很快升高，油漆不致流下来造成厚薄不匀。又如钻井泥浆也要求有良好的触变性，钻井时希望泥浆黏度低，这样泥浆冲刷力强，泵效率高，有利于提高钻井速度。但是一旦停钻以后，就希望泥浆黏度迅速升高，不然泥浆所携带的矿屑等杂质就要沉到井底而形成卡钻事故。

还有一种负触变现象，它与通常的触变性相反，即在外切力作用下，系统的黏度迅速上升，静止后又恢复原状，它是具有时间因素的切稠现象。从滞后圈来看，它是顺时针的，而触变系统是逆时针的。最初发现负触变性是在高分子溶液中，最典型的是5%聚异丁烯的苯溶液。

震凝性系统是溶胶在外界有节奏的震动下变成凝胶。这种节奏性震动可以是轻轻敲打、有规则的圆周运动或搅拌等。例如将1．3%的蒙脱土悬浮体放入1 cm直径的试管内，加一滴饱和NaCI(或KCl)溶液，用橡皮棒有节奏地轻轻敲打试管，在25℃时经过15 S就凝结成凝胶。

震凝性与胀性不同，胀性系统的特点是当外切力取消后，系统的黏度立即降低而“稀化”，而震凝性系统则不同，当外切力去除后，系统仍保持凝固状态，至少有一段时间呈凝聚状态，然后再稀化。从微观结构来看，胀性系统的悬浮体是“高浓度”的，固体含量常高达40%以上，润湿性能良好。震凝性固体含量低，仅1%～2%左右，而且粒子是不对称的，因此形成凝胶完全是粒子定向排列的结果。1

典型特征触变性揭示的是材料的黏度随时间的变化关系。触变性流体具有如下典型特征：

①从静止的物料开始剪切或从低到高改变物料的剪切速率时，黏度随时间降低；

②剪切停止后或从高到低改变物料的剪切速率时，黏度随时间恢复；

③保持剪切速率不变直到应力达到恒定值，可得到平衡流变曲线；

④反复循环剪切可得到滞后环；

⑤无限重复循环剪切可得到平衡滞后环。

以上5种触变性特征现象从不同的方面反映了触变体的流变行为。2

触变性与剪切变稀的区别材料的触变性和剪切变稀特性是两个不同的概念，前者是黏度随剪切时间的变化关系，后者是指稳态剪切黏度随剪切速率的变化关系。材料的反触变性和剪切增稠特性也是两个不同的概念，不能混淆。材料或流体滞后环的差异，与材料的结构差异、受力历史密切相关。2

典型滞后环材料的滞后环可分为正触变环、黏弹环、含黏弹～正触变环的滞后环、含黏弹环、应力过冲和正触变环的滞后环以及含黏弹环、应力过冲和正反触变环的滞后环。

触变性是含结构材料重要而复杂的依时特性。材料受到剪切后，材料内部结构逐渐破坏，当剪切除去后，材料的结构逐渐形成；由于材料结构破坏速率和结构形成速率不同，产生滞后环。当结构形成速率大于结构破坏速率时，材料表现为黏度上升，反之则黏度下降；当二者处于动态平衡状态时，溶液表现为平衡黏度。2

触变性与黏弹性的关系值得指出的是，黏弹性流体经过三角波剪切后，可以得到一个类似反触变环的滞后环(真实的实验现象)，说明受剪前后黏弹性材料结构变化速率存在差异，与受剪切历史有关。

将触变性和黏弹性严格地区分开来十分困难，因为二者都是依赖于时间的现象，都与流体结构变化密切相关。同一种材料可同时体现出黏弹性和触变性，由于所受剪切条件不同，表现出不同的性质。一般在低剪切速率范围内表现黏弹性，而在中等剪切速率以上表现触变性。材料表现滞后环所用剪切速率的大小与材料种类有关。至今仍是一个研究热点和难点。2

触变性的表征为了描述非牛顿流体的触变性行为，提出各种不同的触变模型。其中具有代表性的有Huang方程、5参数黏弹一触变性流体本构方程等。同时含黏弹环和正触变环的滞后环的数学表征。

对无弹性的触变性流体，存在聚集体和单体之间的相互转化过程。当剪切应力作用于该流体时，聚集体结构逐渐解离为单体；当剪切应力消除时，单体将相互作用形成聚集体。由于聚集体结构破坏速率和恢复速率不一致，才表现出触变性。

当剪切应力作用于流体上时，产生的剪切速率为多。该应力分别引起黏性流动，弹性变形和聚集体的解离2。