[科普中国]-二阶带通滤波器

最简单的带通滤波器称之为"二阶带通滤波器"，它的的特性用二阶线性微分方程表示，方程的左边与一般二阶系统的标准形式完全相同，而右边是激励源的导数项。如果激励源通过一个电阻R、电感L及电容C构成一个串联回路，并以电阻两端的电压作为响应，就构成了一个以二阶微分方程描述的“二阶带通滤波器”。

带通滤波器概述一个模拟带通滤波器的例子是电阻-电感-电容电路（RLC circuit）。这些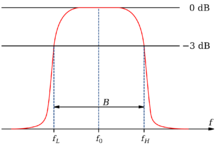滤波器也可以用低通滤波器同高通滤波器组合来产生。

一个理想的滤波器应该有一个完全平坦的通带，例如在通带内没有增益或者衰减，并且在通带之外所有频率都被完全衰减掉，另外，通带外的转换在极小的频率范围完成。实际上，并不存在理想的带通滤波器。滤波器并不能够将期望频率范围外的所有频率完全衰减掉，尤其是在所要的通带外还有一个被衰减但是没有被隔离的范围。这通常称为滤波器的滚降现象，并且使用每十倍频的衰减幅度dB来表示。通常，滤波器的设计尽量保证滚降范围越窄越好，这样滤波器的性能就与设计更加接近。然而，随着滚降范围越来越小，通带就变得不再平坦—开始出现“波纹”。这种现象在通带的边缘处尤其明显，这种效应称为吉布斯现象（Gibbs phenomenon）。

除了电子学和信号处理领域之外，带通滤波器应用的一个例子是在大气科学领域，很常见的例子是使用带通滤波器过滤最近3到10天时间范围内的天气数据，这样在数据域中就只保留了作为扰动的气旋。

在频带较低的截止频率f1和较高的截止频率f2之间是共振频率，这里滤波器的增益最大，滤波器的带宽就是f2和f1之间的差值。1

吉布斯现象吉布斯现象（英语：Gibbs phenomenon），由Henry Wilbraham于1848年最先提出，并由约西亚·吉布斯于1899年证明。在工程应用时常用有限正弦项正弦波叠加逼近原周期信号。所用的谐波次数N的大小决定逼近原波形的程度，N增加，逼近的精度不断改善。但是由于对于具有不连续点的周期信号会发生一种现象：当选取的傅里叶级数的项数N增加时，合成的波形虽然更逼近原函数，但在不连续点附近会出现一个固定高度的过冲，N越大，过冲的最大值越靠近不连续点，但其峰值并不下降，而是大约等于原函数在不连续点处跳变值的9%，且在不连续点两侧呈现衰减振荡的形式。2

双二阶滤波器双二阶滤波器的传递函数有如下的形式：

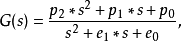
或

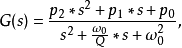分子二项式中系数 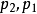决定滤波器的类型。3

参见带阻滤波器

高通滤波器

低通滤波器

双二阶滤波器

原子线滤波器（Atomic line filter）

本词条内容贡献者为:

王伟 - 副教授 - 上海交通大学