[科普中国]-有效磁导率

有效磁导率是一个物理专业术语，用μeff表示，与激励频率f和导体半径r、电导率σ、磁导率μ有关。此概念由德国Forster提出，有效磁导率的实际应用使阻抗分析的问题大大简化，因此应用广泛。

概念提出进行电涡流检测时，检测线圈视在阻抗的变化源于磁场的变化。但分析磁场比较复杂，为简化电涡流检测中的阻抗分析问题，德国Forster提出了有效磁导率的概念。用通以交变电流的无限长圆筒形线圈内置一外径充满线圈的导电圆柱体来分析。1

因为引起检测线圈阻抗发生变化的直接原因是线圈中磁场的变化，所以，在对检测线圈阻抗进行分析时，首先需要分析和计算工件放入检测线圈后磁场的变化情况，然后得到检测线圈阻抗的变化（或称线圈感应电压的变化），才能对工件的各种影响因素进行分析。在长期进行涡流检测理论的研究和实验分析中，福斯特提出了有关有效磁导率的概念。尽管学术界对这一理论的物理意义和表现方式有不同看法，但由于有效磁导率的实际应用使阻抗分析的问题大大简化，因此，得到广泛的应用。

计算方式在半径为r、磁导率为μ、电导率为的σ长直圆柱导体上，紧贴密绕一螺线管线圈。在螺线管中通以交变电流，圆柱导体中会产生一交变磁场，由于趋肤效应，磁场在圆柱导体的横截面上的分布是不均匀的。Forster提出了一个假想模型。圆柱导体的整个截面上有一个恒定不变的均匀磁场，而磁导率却在截面上沿径向变化，它所产生的磁通量等于圆柱导体内真实的物理场所产生的磁通量。这样，就用一个恒定的磁场和变化着的磁导率替代了实际上变化着的磁场和恒定的磁导率，这个变化着的磁导率便称为有效磁导率，用μeff表示，同时推导出它的表达式为：

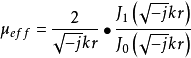式中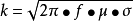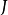，；为贝赛尔函数，它是利用柱坐标求解涉及在圆、球与圆柱内的势场的物理问题时出现的一类特殊函数。1

零阶贝赛尔函数：

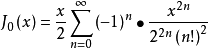一阶贝赛尔函数：

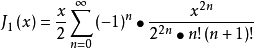
意义因为引起检测线圈阻抗发生变化的直接原因是线圈中磁场的变化，所以，在对检测线圈阻抗进行分析时，首先需要分析和计算工件放入检测线圈后磁场的变化情况，然后得到检测线圈阻抗的变化（或称线圈感应电压的变化），才能对工件的各种影响因素进行分析。在长期进行涡流检测理论的研究和实验分析中，福斯特提出了有关有效磁导率的概念。尽管学术界对这一理论的物理意义和表现方式有不同看法，但由于有效磁导率的实际应用使阻抗分析的问题大大简化，因此，得到广泛的应用。2

本词条内容贡献者为:

杜强 - 高级工程师 - 中国科学院工程热物理研究所