[科普中国]-向量分析

向量分析是数学的分支，关心拥有两个维度或以上的向量的多元实分析。它有一套方程式及难题处理技巧对物理学及工程学特别有帮助。在微分几何与偏微分方程的研究中起着重要作用。它被广泛应用于物理和工程中，特别是在描述电磁场、引力场和流体流动的时候。

简介向量分析关注向量场的微分和积分，主要在3维欧几里得空间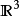 中。“向量分析”有时用作多元微积分的代名词，其中包括向量分析，以及偏微分和多重积分等更广泛的问题。

向量分析从四元数分析发展而来，由约西亚·吉布斯和奥利弗·黑维塞于19世纪末提出，大多数符号和术语由吉布斯和黑维塞在他们1901年的书《向量分析》中提出。向量演算的常规形式中使用外积，不能推广到更高维度，而另一种几何代数的方法，它利用可以推广的外积，下文将会讨论。

相关应用1.代数运算向量分析中的基本代数（非微分）运算的称为向量代数，定义在向量空间，然后应用到整个向量场，包括：

1.标量乘法

标量场和向量场相乘，产生向量场： ；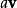

2.向量加法

两个向量场相加，产生向量场： ；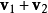

3.内积

两个向量场相乘，产生标量场： ；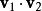

4.外积

两个向量场相乘，产生向量场： ；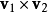

5.标量三重积

向量和两个向量叉积的点积： ；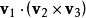

6.向量三重积

向量和两个向量叉积的叉积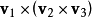： 或 ；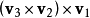

尽管三重积不常作为基本运算，不过仍可以用内积及外积表示1。

2.微分运算向量分析研究定义在标量场或向量场定义的不同微分算子，通常用的向量算子（∇）来表示，也被称为“Nabla算子”。向量分析的五个最重要的微分运算2：

|| ||

3.相关定理同样，也有几个与这几个相关的重要定理，将微积分基本定理拓展到了更高维度：

|| ||

扩展保守向量场

螺线向量场

同源理论

四元数

本词条内容贡献者为:

武伟 - 高级工程师 - 天津直升机有限责任公司