随机量,即随机变量(random variable)表示随机试验各种结果的实值单值函数。随机事件不论与数量是否直接有关,都可以数量化,即都能用数量化的方式表达。
定义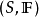 给定样本空间,如果其上的实值函数
给定样本空间,如果其上的实值函数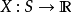 是
是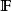 (实值)可测函数,则称
(实值)可测函数,则称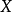 为(实值)随机变量。初等概率论中通常不涉及到可测性的概念,而直接把任何
为(实值)随机变量。初等概率论中通常不涉及到可测性的概念,而直接把任何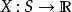 的函数称为随机变量。
的函数称为随机变量。
如果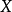 指定给概率空间
指定给概率空间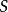 中每一个事件
中每一个事件 有一个实数
有一个实数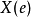 ,同时针对每一个实数
,同时针对每一个实数 都有一个事件集合与其相对应,其中
都有一个事件集合与其相对应,其中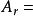 {
{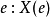 },那么
},那么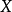 被称作随机变量。随机变量一般用大写拉丁字母或小写希腊字母(比如
被称作随机变量。随机变量一般用大写拉丁字母或小写希腊字母(比如 )来表示,从上面的定义注意到,随机变量实质上是函数,不能把它的定义与变量的定义相混淆,另外概率函数
)来表示,从上面的定义注意到,随机变量实质上是函数,不能把它的定义与变量的定义相混淆,另外概率函数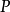 并没有在考虑之中。
并没有在考虑之中。
例如,随机掷两个骰子,整个事件空间可以由36个元素组成:
 这里可以构成多个随机变量,比如随机变量
这里可以构成多个随机变量,比如随机变量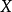 (获得的两个骰子的点数和)或者随机变量
(获得的两个骰子的点数和)或者随机变量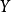 (获得的两个骰子的点数差),随机变量
(获得的两个骰子的点数差),随机变量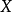 可以有11个整数值,而随机变量
可以有11个整数值,而随机变量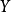 只有6个。
只有6个。
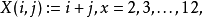
又比如,在一次扔硬币事件中,如果把获得的背面的次数作为随机变量 ,则
,则 可以取两个值,分别是0和1。
可以取两个值,分别是0和1。
如果随机变量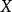 的取值是有限的或者是可数无穷尽的值
的取值是有限的或者是可数无穷尽的值
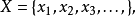 则称
则称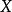 为离散随机变量。 如果{\displaystyle X}由全部实数或者由一部分区间组成,
为离散随机变量。 如果{\displaystyle X}由全部实数或者由一部分区间组成,
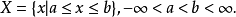 则称
则称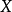 为连续随机变量,连续随机变量的取值是不可数及无穷尽的。1
为连续随机变量,连续随机变量的取值是不可数及无穷尽的。1
性质不确定性随机变量在不同的条件下由于偶然因素影响,其可能取各种随机变量不同的值,具有不确定性和随机性,但这些取值落在某个范围的概率是一定的,此种变量称为随机变量。随机变量可以是离散型的,也可以是连续型的。如分析测试中的测定值就是一个以概率取值的随机变量,被测定量的取值可能在某一范围内随机变化,具体取什么值在测定之前是无法确定的,但测定的结果是确定的,多次重复测定所得到的测定值具有统计规律性。随机变量与模糊变量的不确定性的本质差别在于,后者的测定结果仍具有不确定性,即模糊性。2
基本类型简单地说,随机变量是指随机事件的数量表现。某地若干名男性健康成人中,每人血红蛋白量的测定值;等等。另有一些现象并不直接表现为数量,例如人口的男女性别、试验结果的阳性或阴性等,但我们可以规定男性为1,女性为0,则非数量标志也可以用数量来表示。这些例子中所提到的量,尽管它们的具体内容是各式各样的,但从数学观点来看,它们表现了同一种情况,这就是每个变量都可以随机地取得不同的数值,而在进行试验或测量之前,我们要预言这个变量将取得某个确定的数值是不可能的。 按照随机变量可能取得的值,可以把它们分为两种基本类型:
1.离散型随机变量: 即在一定区间内变量取值为有限个,或数值可以一一列举出来。例如某地区某年人口的出生数、死亡数,某药治疗某病病人的有效数、无效数等。
2.连续型随机变量: 即在一定区间内变量取值有无限个,或数值无法一一列举出来。例如某地区男性健康成人的身长值、体重值,一批传染性肝炎患者的血清转氨酶测定值等。3
随机变量的函数概述一个新的随机变量能被波莱尔可测函数定义 来产生一个随机变量X.Y的累积分布函数是:
来产生一个随机变量X.Y的累积分布函数是:
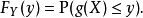 如果波莱尔函数可逆:
如果波莱尔函数可逆:
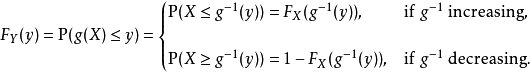 得到它的概率密度函数:
得到它的概率密度函数:
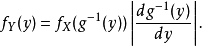
例子定义X为实数,在连续性随机变量里,让Y=X,
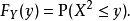 如果y
如果y
 如果y≥ 0,
如果y≥ 0,
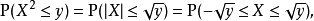 可以得到:
可以得到:
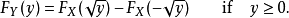
参见概率论
随机分布
随机性
随机向量
随机函数
生成函数
算法信息论
随机变量的收敛
本词条内容贡献者为:
尚华娟 - 副教授 - 上海财经大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国