[科普中国]-均值定理

均值定理，又称基本不等式。主要内容为在正实数范围内，若干数的几何平均数不超过他们的算术平均数，且当这些数全部相等时，算术平均数与几何平均数相等。

均值定理是高中数学学习中的一个非常重要的知识点，在函数求最值问题中有十分频繁的应用。

定义均值定理：对于任意两个正实数a、b，都有

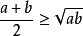
当且仅当a=b时，等号成立。
注**：运用均值不等式求最值条件**

① ， ；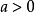

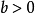②a和b的乘积ab是一个定值（正数）；

③等号成立条件。

相关重要不等式：

① ；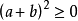

② ；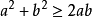

③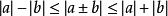 。1

几何含义一个矩形的长为a，宽为b，画两个正方形，要求第一个正方形的面积与矩形的面积相同，第二个正方形的周长与矩形的周长相同，如图1所示。第一个正方形的面积为ab，则其边长为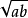 ；第二个正方形的周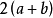长为 ，边长为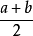 。可以看出第一个正方形面积不大于第二个正方形，即边长关系 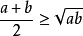。2

推广均值不等式

均值定理可进行推广，得到更为通用的均值不等式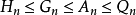： 。即调和平均数不超过几何平均数，几何平均数不超过算术平均数，算术平均数不超过平方平均数，简记为“调几算方”。

其中：对于任意非负实数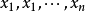 ，有

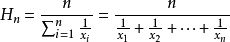，即调和平均数；

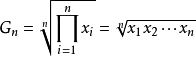，即几何平均数；

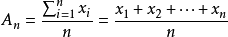，即为算术平均数；

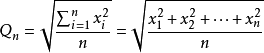，即为平方平均数。

例题（1）当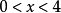 时，求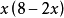 的最大值。1

解：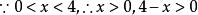

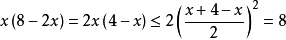
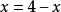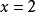当且仅当 ，即 时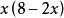， 取最大值8。

（2）当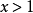 时，求函数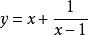 的最小值。

解：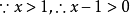

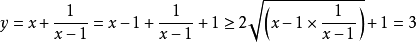
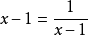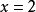当且仅当，即时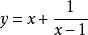，取最小值3。

本词条内容贡献者为:

尚华娟 - 副教授 - 上海财经大学